揭秘:一立方的计算方法详解
一立方怎么算
在日常生活中,我们经常会遇到需要计算体积的情况,尤其是当我们需要了解某个物体占据的空间大小时,“一立方”这个概念就显得尤为重要。那么,一立方究竟是怎么算出来的呢?本文将详细解释一立方的计算方法,并通过实例帮助大家更好地理解这一概念。
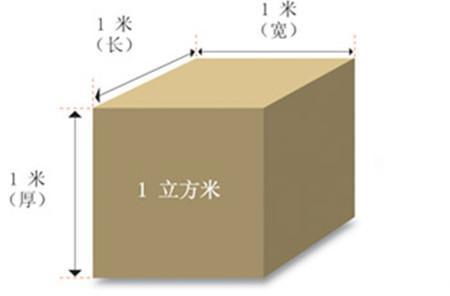
一、立方体的定义与特点
首先,我们需要明确什么是立方体。立方体是一种特殊的六面体,它的六个面都是正方形,并且所有棱的长度都相等。换句话说,立方体是一个三维空间中的正方形“盒子”。
立方体的特点包括:
1. 有六个面,每个面都是正方形。
2. 有十二条棱,每条棱的长度都相等。
3. 有八个顶点,每个顶点都是三条棱的交点。
二、立方体的体积公式
要计算立方体的体积,我们需要用到一个简单而重要的公式:
体积 V = a³
其中,a 代表立方体的棱长。这个公式告诉我们,立方体的体积等于其棱长的三次方。
三、如何计算一立方
现在,我们知道了立方体的体积公式,那么如何计算一立方呢?实际上,“一立方”通常指的是边长为1单位的立方体的体积。在这个情况下,棱长 a = 1,所以:
体积 V = 1³ = 1 立方单位
这里的“立方单位”可以是任何你选择的单位,比如立方米(m³)、立方厘米(cm³)、立方英寸(in³)等。只要棱长是1,那么体积就是一立方单位。
四、实例解析
为了更好地理解一立方的计算,我们可以通过几个实例来进行分析。
实例一:计算边长为2米的立方体的体积
1. 确定棱长:a = 2米
2. 应用公式:V = a³ = 2³ = 8 立方米
所以,边长为2米的立方体的体积是8立方米。
实例二:计算边长为0.5米的立方体的体积
1. 确定棱长:a = 0.5米
2. 应用公式:V = a³ = (0.5)³ = 0.125 立方米
所以,边长为0.5米的立方体的体积是0.125立方米,也可以理解为1/8立方米。
实例三:计算边长为10厘米的立方体的体积
1. 确定棱长:a = 10厘米 = 0.1米(注意单位转换)
2. 应用公式:V = a³ = (0.1)³ = 0.001 立方米 = 1000 立方厘米
所以,边长为10厘米的立方体的体积是1000立方厘米,也可以转换为0.001立方米。
五、其他形状体积的计算方法
虽然本文重点讲解的是立方体的体积计算,但在实际生活中,我们可能会遇到各种形状的物体,需要计算它们的体积。以下是一些常见形状的体积计算方法:
1. 长方体:体积 V = 长 × 宽 × 高
长方体的体积计算相对简单,只需要将长、宽、高三个维度相乘即可。
2. 球体:体积 V = (4/3)πr³
其中,r 是球体的半径。这个公式告诉我们,球体的体积与其半径的三次方成正比。
3. 圆柱体:体积 V = πr²h
其中,r 是圆柱体的底面半径,h 是圆柱体的高。这个公式表明,圆柱体的体积等于其底面积乘以高。
4. 圆锥体:体积 V = (1/3)πr²h
其中,r 是圆锥体的底面半径,h 是圆锥体的高。与圆柱体类似,圆锥体的体积也与其底面积有关,但因为是三维空间中的“尖顶”形状,所以体积是圆柱体体积的1/3。
六、实际应用中的注意事项
在计算物体的体积时,我们需要注意以下几点:
1. 单位统一:确保所有参与计算的长度单位都是统一的。如果单位不同,需要先进行单位转换。
2. 精度要求:根据实际需要选择合适的精度进行计算。在某些情况下,过于精确的计算可能并不必要,反而会增加计算复杂度。
3. 形状近似:对于非规则形状的物体,可能需要通过近似计算来得到其体积。这通常涉及到将物体分割成多个规则形状的部分,然后分别计算这些部分的体积并求和。
七、总结
通过本文的讲解,我们了解了立方体的定义、特点以及体积计算公式。同时,我们也学会了如何计算一立方(即边长为1单位的立方体的体积)。此外,我们还简要介绍了其他常见形状的体积计算方法以及在实际应用中的注意事项。希望这些内容
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/07
-
03/07
-
03/07
-
03/07
-
03/07










