揭秘勾股定理：多种证明方法，你了解几种？

勾股定理，作为数学史上的一颗璀璨明珠，自古以来便吸引了无数数学家和爱好者的目光。这一揭示直角三角形三边关系的定理，不仅在数学领域内占有举足轻重的地位，更在物理、工程等多个领域发挥着不可替代的作用。本文将深入探讨证明勾股定理的多种方法，旨在为读者提供一个全面而深入的理解。

勾股定理的基本表述是：在一个直角三角形中，直角边的平方和等于斜边的平方。用数学公式表示即为a² + b² = c²，其中a和b为直角三角形的两条直角边，c为斜边。这一简洁而深刻的公式，背后隐藏着多种不同的证明方法，每一种都体现了数学家的智慧和创造力。

方法一：欧几里得证法

欧几里得在其著作《几何原本》中给出了勾股定理的证明，这是最为人熟知的一种方法。证明过程大致如下：构造一个边长为a+b的正方形，并划分为四个全等的直角三角形、一个边长为a的正方形、一个边长为b的正方形。通过比较面积，可以发现四个直角三角形的总面积加上边长为a和b的两个正方形的面积，等于边长为a+b的大正方形的面积。由此，可以推导出a² + b² = c²的公式。

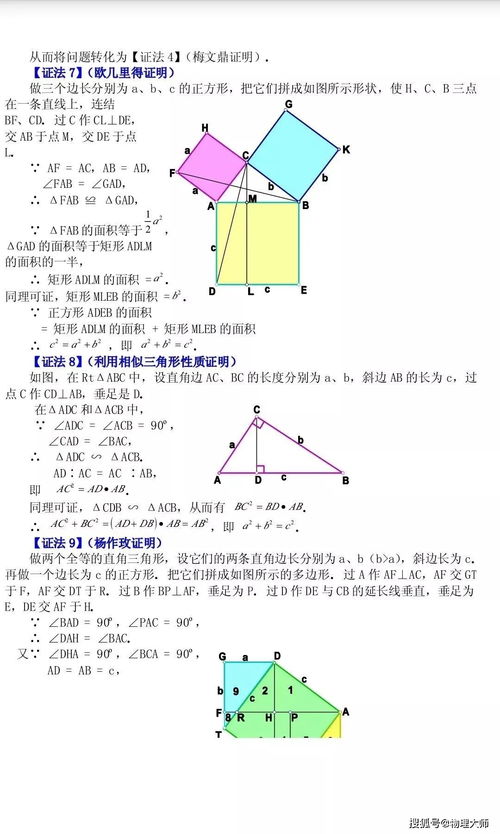
方法二：赵爽弦图证法

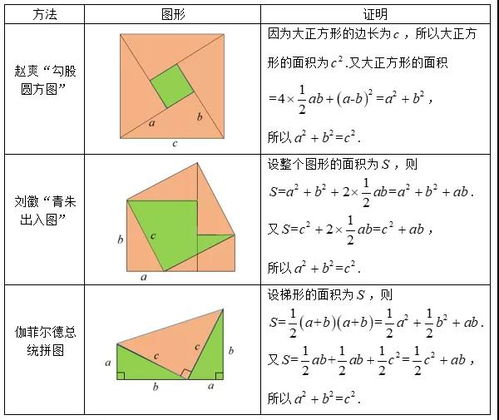
在中国古代，数学家赵爽也给出了勾股定理的一种证明方法，即赵爽弦图法。这种方法利用了四个全等的直角三角形和一个内接正方形，通过比较面积来证明勾股定理。具体步骤如下：将四个全等的直角三角形围绕一个正方形排列，使得它们的直角边分别与正方形的两边重合。这样，四个直角三角形的总面积加上正方形的面积，就等于外围一个大正方形的面积。通过计算可以发现，大正方形的面积等于直角三角形的斜边c的平方，而内部小正方形的面积加上四个直角三角形的面积则等于直角边a和b的平方和。因此，可以推导出a² + b² = c²。

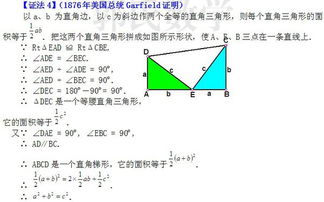
方法三：总统证法

总统证法，又称加菲尔德证法，是由美国第二十任总统加菲尔德在1876年给出的一种简洁明了的证明方法。这种方法利用了一个梯形和两个直角三角形的面积关系来证明勾股定理。具体步骤如下：构造一个梯形，其上底为a，下底为b，高为a+b，并在梯形内部构造两个全等的直角三角形，使得它们的直角边分别等于梯形的上底和下底。通过计算梯形的面积和两个直角三角形的面积之和，可以发现它们相等，从而推导出a² + b² = c²的公式。

方法四：割补证法

割补证法是一种通过图形的切割和拼接来证明勾股定理的方法。这种方法通常涉及到一个直角三角形、一个正方形和几个全等的三角形或四边形。具体步骤如下：将直角三角形的斜边延长至某一点，并在延长线上作一个正方形。然后，将这个正方形与直角三角形进行切割和拼接，形成一个新的图形。通过计算新图形的面积和各个部分的面积之和，可以发现它们相等，从而推导出a² + b² = c²的公式。

方法五：欧几里得引理证法

欧几里得引理是证明勾股定理的一种重要工具。这种方法通过构造辅助线和利用已知条件来证明勾股定理。具体步骤如下：在直角三角形中，作一条垂直于斜边的高，将直角三角形分为两个小的直角三角形。然后，利用三角形的相似性质和面积关系，可以推导出直角边的平方和等于斜边的平方。这种方法虽然较为繁琐，但具有较高的普适性和灵活性。

方法六：费马证法

费马是法国著名的数学家和物理学家，他提出了一种利用无穷递降法来证明勾股定理的方法。这种方法虽然较为抽象和复杂，但展示了数学中的一种重要思维方式。具体步骤如下：假设存在一个满足a² + b² = nc²（n≠1）的直角三角形，然后通过一系列的数学变换和推理，最终得到一个更小的直角三角形也满足同样的关系。由于这个过程可以无限进行下去，因此与原假设矛盾。由此可以推断出，不存在满足a² + b² = nc²（n≠1）的直角三角形，从而证明了a² + b² = c²的公式。

方法七：旋转证法

旋转证法是一种通过图形的旋转和拼接来证明勾股定理的方法。这种方法通常涉及到一个直角三角形和一个正方形或矩形。具体步骤如下：将直角三角形的直角边之一作为正方形的边长，然后将直角三角形绕直角边旋转90度。这样，就可以得到一个由直角三角形和正方形组成的新的图形。通过计算新图形的面积和各个部分的面积之和，可以发现它们相等，从而推导出a² + b² = c²的公式。

方法八：面积法

面积法是一种直接利用三角形的面积公式来证明勾股定理的方法。这种方法虽然简单直观，但需要一定的数学基础。具体步骤如下：在直角三角形