Excel标准差计算：掌握公式与函数

在数据处理和分析的过程中，Excel作为一款功能强大的电子表格软件，被广泛应用于各个领域。其中，标准差作为一个重要的统计量，用于衡量数据的离散程度。本文将深入探讨Excel中标准差公式函数的应用，帮助读者更好地理解和使用这一工具。

标准差，简而言之，是衡量数据分布离散程度的一个指标。一个较低的标准差表示数据点比较接近平均值，而一个较高的标准差则表示数据点较为分散。在Excel中，计算标准差主要通过两个函数实现：STDEV.P和STDEV.S。前者用于计算基于整个数据集的总体标准差，后者则用于计算基于样本的标准差。了解这两者之间的区别对于正确应用公式至关重要。

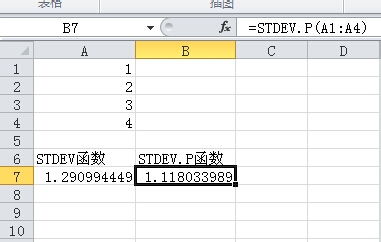
STDEV.P函数适用于当你拥有全部数据集时。它计算的是数据的总体标准差，假设你处理的是整个总体而非从中抽取的样本。STDEV.P函数的使用相对简单，你只需要将要计算的数据范围作为参数输入即可。例如，如果你的数据在A1到A10的单元格中，你可以通过输入“=STDEV.P(A1:A10)”来计算这些数据的总体标准差。值得注意的是，当数据集中包含有重复值时，STDEV.P依然能够准确计算出标准差，因为它考虑的是所有数据点的整体分布情况。

与STDEV.P不同，STDEV.S函数是用于计算样本标准差的。在统计学中，样本是从总体中随机抽取的一部分数据，用于推断总体的特性。由于样本仅代表总体的一部分，因此使用样本标准差时需要采用特定的计算方法，以避免偏差。在Excel中，STDEV.S函数能够自动调整计算公式，以适应样本数据的特性。使用该函数时，你同样需要将数据范围作为参数输入，例如“=STDEV.S(A1:A10)”。通过这种方式，你可以得到基于给定样本的标准差估计值，这对于统计分析和预测非常有用。

除了这两个基本的标准差函数外，Excel还提供了一些辅助函数，用于更深入地分析数据的离散程度。例如，VAR.P和VAR.S函数分别用于计算总体方差和样本方差。方差是标准差的平方，同样用于衡量数据的离散程度，但在某些统计分析中，方差可能具有更直接的解释意义。通过计算方差，你可以了解数据点与平均值的平方距离，这对于评估数据的波动性和稳定性非常有帮助。在Excel中，使用VAR.P和VAR.S函数的方法与STDEV.P和STDEV.S类似，只需将相应的数据范围作为参数输入即可。

在实际应用中，标准差的计算和分析往往需要结合其他统计工具和方法。例如，通过绘制直方图或箱线图，你可以直观地看到数据的分布情况，以及标准差如何影响数据的离散程度。直方图通过显示数据点的频率分布，帮助你了解数据的集中趋势和分散程度。而箱线图则通过展示数据的五个关键统计量（最小值、第一四分位数、中位数、第三四分位数和最大值），提供了一种简洁明了的数据可视化方法。结合标准差的分析，你可以更深入地理解数据的特性和潜在规律。

此外，在进行数据分析时，还需要注意数据的预处理和清洗工作。例如，检查数据集中是否存在异常值或缺失值，这些都会对标准差的计算结果产生影响。异常值是指那些与大多数数据点显著不同的值，它们可能是由于测量误差或数据录入错误等原因产生的。在处理异常值时，你需要根据具体情况进行判断，是将其保留、删除还是进行某种形式的修正。同样，缺失值也需要得到妥善处理，以确保标准差的计算结果准确无误。

在实际操作中，Excel提供了多种工具和方法来帮助你进行数据的预处理和清洗工作。例如，你可以使用条件格式来突出显示异常值或缺失值，以便更容易地发现和处理它们。此外，Excel还提供了数据筛选和排序功能，帮助你根据特定条件筛选数据，并对数据进行排序，以便更直观地了解数据的分布情况和潜在规律。

值得一提的是，Excel的标准差函数和方差函数都具有内置的错误检查机制。当你输入的数据范围无效或包含非数值数据时，这些函数会返回错误值（如VALUE!、NUM!等）。这有助于你及时发现数据输入或公式使用中的问题，并进行相应的修正。因此，在使用这些函数时，建议始终关注Excel返回的结果，以确保数据分析的准确性和可靠性。

总的来说，Excel中的标准差公式函数是数据分析领域不可或缺的工具之一。通过学习和掌握这些函数的使用方法，你可以更好地理解和分析数据的离散程度，从而发现数据中的潜在规律和趋势。无论是在学术研究、商业分析还是其他领域，掌握Excel标准差函数的应用都将为你提供有力的支持。因此，建议读者在实践中不断尝试和应用这些函数，以提升自己的数据分析能力和水平。