向量a与向量b的乘积公式是什么

在数学的广阔天地中，向量作为描述空间方向与大小的有力工具，扮演着举足轻重的角色。而向量的数量积，即我们通常所说的“向量a乘向量b”，更是连接几何与代数的一座桥梁，它不仅揭示了向量之间的夹角关系，还蕴含着丰富的物理意义和应用价值。本文将从定义、几何意义、物理背景、代数性质以及应用实例等多个维度，深入探讨向量a乘向量b的奥秘。

定义篇：向量数量积的基石

向量a与向量b的数量积，又称点积或内积，其定义如下：设向量a的坐标为(a1, a2, ..., an)，向量b的坐标为(b1, b2, ..., bn)，则向量a与向量b的数量积为a·b = a1b1 + a2b2 + ... + anbn。这一简洁的公式背后，隐藏着向量之间深刻的内在联系。值得注意的是，向量数量积的结果是一个标量（即没有方向的数值），而非向量。

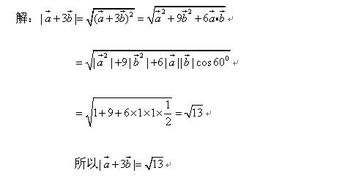
几何意义篇：夹角与投影的桥梁

向量数量积的几何意义，在于它直接关联了向量的长度与它们之间的夹角。具体来说，向量a与向量b的数量积等于向量a的模长乘以向量b在向量a上的投影长度（或反之），再乘以两向量夹角θ的余弦值，即a·b = |a| × |b| × cosθ。这一关系不仅提供了计算两向量夹角的方法（通过反余弦函数arccos(a·b / (|a| × |b|))求得），还揭示了向量在特定方向上的投影长度，这对于理解向量的空间分布和相互作用至关重要。

物理背景篇：力与功的纽带

向量数量积在物理学中的应用尤为广泛，它成为连接力与功、电场与电荷、磁场与电流等物理概念的纽带。以力与功为例，当一个力F作用于一个物体上，使其沿位移s移动时，该力所做的功W可以通过F与s的数量积来计算，即W = F·s。若力F与位移s方向一致，则功为正；若方向相反，则功为负；若两者垂直，则功为零，因为此时力在位移方向上没有产生任何效果。这一原理不仅适用于机械功的计算，也是能量守恒与转换定律的基础之一。

代数性质篇：运算规则的探索

向量数量积遵循一系列代数性质，这些性质不仅简化了计算，也深化了我们对向量运算的理解。例如，交换律：a·b = b·a；分配律：(ka + lb)·c = ka·c + lb·c（其中k、l为标量）；以及当且仅当两向量平行（包括同向或反向）时，它们的数量积才满足乘法分配律的逆命题，即若a·(b + c) = a·b + a·c且b ≠ -c，则必有a、b、c共线。此外，零向量的数量积为零，即0·a = 0，这进一步强化了向量空间结构的完整性。

应用实例篇：从理论到实践的跨越

向量数量积的应用，跨越了数学、物理、工程乃至计算机科学等多个领域，以下列举几例以窥全豹：

1. 图像处理：在计算机视觉中，向量数量积可用于计算图像像素间的相似度，从而进行图像匹配、边缘检测等任务。例如，通过比较两个像素向量a和b的数量积，可以判断它们是否属于同一物体或背景。

2. 机器学习：在支持向量机（SVM）等分类算法中，向量数量积是计算样本点与决策边界距离的关键，进而影响模型的分类效果和泛化能力。

3. 力学分析：在结构力学中，向量数量积被用来计算结构件上受到的合力及其方向，这对于设计安全可靠的建筑结构至关重要。

4. 电路设计：在电子工程中，向量数量积可用于计算交流电路中的功率因数，它反映了电能的有效利用率，是优化电路设计、提高能效的关键指标。

5. 地理信息系统：在GIS中，向量数量积可用于分析地理要素的空间关系，如计算两地点的相对方向或判断路径是否相交，为交通规划、环境监测等领域提供数据支持。

综上所述，向量a乘向量b的数量积，不仅是数学中的一个基础概念，更是连接理论与实践、抽象与具体的桥梁。它以其独特的定义、丰富的几何意义、深厚的物理背景、严谨的代数性质以及广泛的应用实例，展示了向量运算的魅力和价值。通过深入学习向量数量积，我们不仅能更好地掌握数学工具，还能拓宽视野，将数学知识应用于解决实际问题的过程中，从而推动科学技术的进步与发展。