如何计算增长率?
增长率计算公式详解
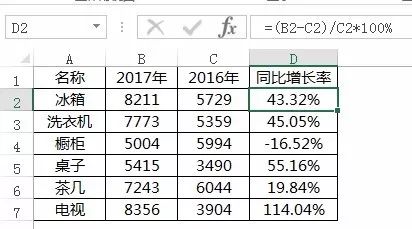
增长率是衡量一个量随时间变化快慢的重要指标,广泛应用于经济、统计、生物学、人口学等众多领域。正确地计算增长率,能够帮助我们更好地理解数据背后的趋势和规律。本文将详细介绍增长率的计算公式,并通过实例进行演示,帮助读者掌握这一技能。
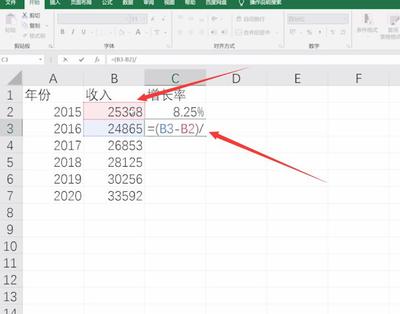
一、增长率的基本概念
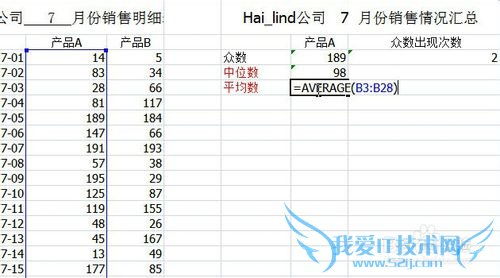
增长率是指一个量在一定时期内增长的幅度与原来数量的比值,通常以百分比的形式表示。它反映了数量增长的速度和幅度,是衡量事物发展趋势的重要指标。

二、增长率的计算公式
增长率的计算公式有多种,具体使用哪种公式取决于所关心的增长类型。以下是几种常见的增长率计算公式:
1. 简单增长率公式
简单增长率是最常用的计算公式,适用于计算两个不同时期之间的增长率。公式如下:
增长率 = (现期数值 - 基期数值) ÷ 基期数值 × 100%
其中,现期数值是现在的数量,基期数值是过去某一时期的数量。
2. 年均增长率公式
年均增长率用于计算一个量在多年内的平均增长速度。公式如下:
年均增长率 = [(末期数值 ÷ 基期数值)^(1/n) - 1] × 100%
其中,n 表示时期数(年数),末期数值是最后一年的数量,基期数值是最初一年的数量。
3. 复合增长率公式
复合增长率用于计算连续多个时期(如季度、月份)的平均增长速度。公式如下:
复合增长率 = [(现期数值 ÷ 基期数值)^(1/n) - 1] × 100%
其中,n 表示时期数(季度数、月数等),现期数值是最后一个时期的数量,基期数值是最初一个时期的数量。
三、增长率公式的应用实例
1. 简单增长率的应用
假设某公司去年销售额为100万元,今年销售额为120万元,求该公司的年增长率。
根据简单增长率公式:
增长率 = (120 - 100) ÷ 100 × 100% = 20%
因此,该公司的年增长率为20%。
2. 年均增长率的应用
假设某城市2010年人口为100万人,2020年人口为150万人,求该城市过去十年的年均增长率。
根据年均增长率公式:
年均增长率 = [(150 ÷ 100)^(1/10) - 1] × 100% ≈ 4.14%
因此,该城市过去十年的年均增长率为4.14%。
3. 复合增长率的应用
假设某公司第一季度销售额为100万元,第四季度销售额为130万元,求该公司前三季度的复合增长率。
根据复合增长率公式:
复合增长率 = [(130 ÷ 100)^(1/3) - 1] × 100% ≈ 9.10%
因此,该公司前三季度的复合增长率为9.10%。
四、增长率计算中的注意事项
1. 基期数值的选择
基期数值是增长率计算的基础,应确保选择正确的基期数值。不同的基期数值会导致不同的增长率结果。
2. 时间跨度的确定
时间跨度是增长率计算的关键因素,应根据实际情况确定合适的时间跨度。时间跨度太短可能导致增长率波动较大,时间跨度太长则可能掩盖短期内的变化。
3. 数据的准确性和可比性
增长率计算的数据应准确可靠,并且具有可比性。如果数据存在误差或不可比性,将会影响增长率的计算结果。
4. 增长率与绝对量的关系
增长率反映了数量增长的速度和幅度,但并不能完全代表数量的实际水平。在比较不同数量的增长率时,还需要考虑它们的绝对量。
五、增长率的应用场景
1. 经济领域
在经济学中,增长率常用于衡量GDP、人均收入、工业增加值等经济指标的增长情况。通过计算增长率,可以了解经济发展的速度和趋势。
2. 统计领域
在统计学中,增长率是描述数据变化趋势的重要工具。通过计算增长率,可以发现数据中的异常值、周期性波动等特征。
3. 生物学领域
在生物学中,增长率常用于描述生物种群的增长情况。通过计算增长率,可以了解生物种群的繁殖速度、环境适应性等特征。
4. 人口学领域
在人口学中,增长率用于描述人口数量的变化情况。通过计算增长率,可以预测未来人口数量的趋势和规模。
六、增长率计算中的常见问题
1. 增长率与
游戏攻略帮助你
更多+-
04/05
-
04/05
-
04/05
-
04/05
-
04/05