揭秘曲率：探索几何与物理中的弯曲奥秘

曲率是一个在几何学、物理学、工程学等多个领域中广泛应用的重要概念。简单来说，曲率用于描述一个物体形状在某一点上的弯曲程度。通过对曲率的深入了解和研究，人们可以更好地掌握物体形状的弯曲特性，从而为实际问题提供解决方案。以下是对曲率的详细介绍。

一、曲率的定义

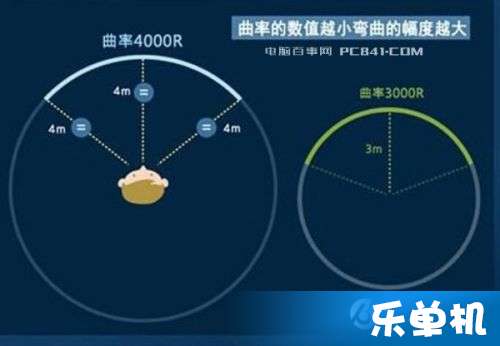
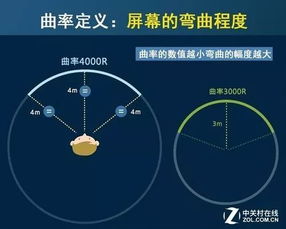
曲率（curvature）是描述曲线上某个点的切线方向角对弧长的转动率，它通过微分来定义，表明曲线偏离直线的程度。在数学上，曲率表示曲线在某一点的弯曲程度的数值。曲率越大，表示曲线的弯曲程度越大；反之，曲率越小，表示曲线越接近直线。

二、曲率的计算

曲率的计算涉及到曲线的参数方程或直角坐标方程。设曲线的直角坐标方程为y=f(x)，且y=f(x)具有二阶导数，那么曲线在点M处的曲率K可以通过以下公式计算：

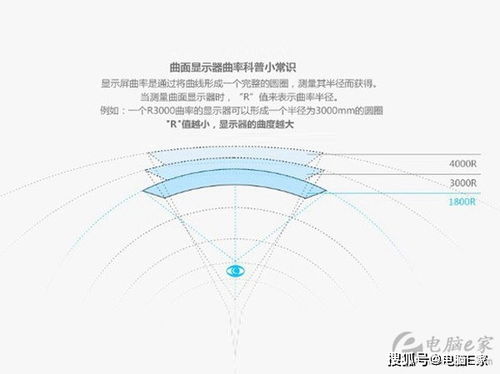
K = |f''(x)| / [(1 + (f'(x))^2)^(3/2)]

如果曲线由参数方程给出，也可以通过参数方程求导法来计算曲率。

三、曲率与曲率半径

曲率与曲率半径是密切相关的两个概念。曲率的倒数就是曲率半径。曲率半径越大，表示曲线在该点附近越平缓；曲率半径越小，表示曲线在该点附近越陡峭。

在实际应用中，常常用曲率圆（也称密切圆）来近似代替曲线在某点附近的一段圆弧。曲率圆的半径就是曲率半径，圆心称为曲率中心。

四、曲率的物理意义

从物理角度来看，曲率描述的是物体法向加速度关于弧长参数的变化。在物体沿曲线运动时，如果速度为单位向量，那么该运动仅有法向加速度（特殊情况就是匀速圆周运动的向心加速度）。法向加速度就是速度的导数，也即切线方向角对弧长的转动率，也就是曲率。

因此，曲率越大，法向加速越明显，物体的轨迹就越“弯”。这一物理意义使得曲率在动力学、运动学等领域具有广泛的应用。

五、曲率的应用领域

曲率作为一个几何学的概念，在多个领域具有重要的应用价值。以下是一些主要的应用领域：

1. 工程设计：在道路设计、桥梁建设、建筑物结构设计等方面，曲率的概念被广泛应用。通过计算曲率，工程师可以更好地理解结构的弯曲特性，从而进行合理的设计和优化。

2. 自然科学：在地球物理、天文学、生物学等方面，曲率也具有重要意义。例如，地球物理学家通过研究地壳的曲率变化，可以了解地壳构造的特点；生物学家通过研究生物体表面的曲率，可以揭示生物形态的特征。

3. 艺术创作：在雕塑、建筑、绘画等方面，曲率也有着举足轻重的地位。通过运用曲率的原理，艺术家可以创作出具有独特美感的作品。例如，建筑大师安东尼·高迪通过研究曲线和曲面的曲率，设计出了许多具有流线型美感的建筑作品。

4. 计算机科学：在计算机图形学、机器学习和计算机视觉等方面，曲率也有广泛的应用。通过计算曲率，可以实现曲面的分段、光顺和拓扑等操作；曲率还可以作为图像和数据的一个重要特征，用于模式分类、图像识别等领域。

5. 经济学：在经济学中，曲率也有着广泛的应用。例如，通过分析需求曲线的曲率，可以判断产品的市场需求量；通过曲线求导法，可以估计某些特定市场的价格弹性；通过曲线优化法，可以解决一些市场的效率问题。

六、曲率与其他概念的关系

1. 弯曲度：弯曲度是指曲线或曲面在某一点处的曲率大小，它用来衡量物体的弯曲程度。而曲率则更加关注曲线或曲面在某一点处的弯曲方向。换句话说，弯曲度描述了物体形状的“弯曲程度”，而曲率描述了物体形状的“弯曲特性”。

2. 曲率张量：曲率张量是一种用于描述曲面在空间中的弯曲特性的数学工具。它可以帮助我们更好地理解曲面的弯曲特性，并与曲率的概念紧密相连。通过计算曲率张量，我们可以了解曲面在不同方向上的曲率变化，从而深入研究其几何特性。

3. 密切圆与渐屈线：密切圆是对曲线在某点附近的最佳圆近似，其半径的倒数就是曲率。而渐屈线则是曲线的一系列密切圆的圆心轨迹，它反映了曲线弯曲程度的变化规律。

七、曲率的计算实例

以下是一个计算曲线曲率的简单实例：

设曲线的直角坐标方程为y = x^2，我们需要计算该曲线在点(1,1)处的曲率。

首先，求出函数f(x) = x^2的一阶导数f'(x) = 2x和二阶导数f''(x) = 2。