揭秘!如何轻松计算根号6的值?
根号6等于多少怎么算
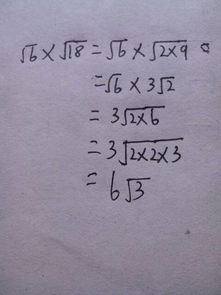
根号6是一个无理数,无法表示为两个整数的比。但我们可以使用多种方法来计算或逼近其值。以下是几种常见的方法:
一、近似计算法
1. 计算器直接计算
使用计算器可以直接得到根号6的近似值。按下根号键(√),然后输入6,即可得到结果。这种方法简单快捷,适用于需要快速得到结果的情况。
2. 手动近似计算
如果没有计算器,可以使用手动近似计算的方法。一种常见的方法是使用连续分数展开式或者泰勒级数展开式。但这里我们介绍一种更直观的方法:利用已知的平方根值进行逼近。
我们知道:
√4 = 2
√9 = 3
因为6在4和9之间,所以根号6的值应该在2和3之间。为了更精确地逼近,可以使用逐步逼近法,例如通过不断调整小数位,或者使用更复杂的逼近算法(如牛顿迭代法)。
二、数学公式法
1. 代数法
根号6可以表示为两个数的乘积的平方根,即√6 = √(2 × 3)。虽然这没有直接给出具体数值,但有助于理解根号6的组成。
2. 级数展开法
使用级数展开法可以得到根号6的近似值。例如,可以使用牛顿-拉弗森迭代法或者泰勒级数展开法。
牛顿-拉弗森迭代法:
选择初始值x0(如x0 = 2.5),然后不断迭代以下公式:
x(n+1) = 0.5 * (x(n) + 6/x(n))
通过多次迭代,可以得到越来越精确的根号6的值。
泰勒级数展开法:
将根号函数在某一点(如x = 2)处展开为泰勒级数,然后代入x = 6进行计算。这种方法比较复杂,通常用于理论分析或编程计算。
三、几何法
根号6在几何中也有应用。例如,在一个边长为√6的正方形中,其对角线的长度就是2√3(或者根号12,但这与根号6直接相关,因为2√3 = √(2^2 * 3) = √12 = 2 * √3 = √4 * √3 = 2 * (√6/√2) = 2√6/2 = √6 的两倍的一个因子)。虽然这种方法不直接给出根号6的值,但有助于理解根号6在几何中的应用。
四、编程计算法
在现代计算中,编程是一种常用的计算根号6的方法。几乎所有编程语言都提供了数学库函数来计算平方根。例如,在Python中,可以使用math.sqrt(6)来得到根号6的值。
```python
import math
result = math.sqrt(6)
print(result)
```
在C语言中,可以使用sqrt函数:
```c
include
include
int main() {
double result = sqrt(6);
printf("%lf\n", result);
return 0;
```
在Java中,可以使用Math.sqrt方法:
```java
public class Main {
public static void main(String[] args) {
double result = Math.sqrt(6);
System.out.println(result);
```
五、精确值表示法
虽然根号6是一个无理数,无法表示为两个整数的比,但我们可以使用无限不循环小数来表示其精确值。通过计算器或编程计算,我们可以得到根号6的无限不循环小数形式。例如:
根号6 ≈ 2.449489742783178
这个值是一个近似值,因为根号6的精确值是一个无限不循环小数。如果需要更高的精度,可以使用更高级的计算工具或算法。
六、实际应用
根号6在多个领域有实际应用。例如:
物理学:在物理学中,根号6经常出现在与空间对角线、力的合成等相关的计算中。
工程学:在工程学中,根号6用于计算结构的稳定性、应力分析等。
计算机科学:在计算机科学中,根号6可能用于图形处理、算法优化等领域。
经济学:在经济学中,根号6可能用于计算标准差、方差等统计量。
结论
根号6是一个无理数,无法表示为两个整数的比。但我们可以使用多种方法来计算或逼近其值,包括计算器直接计算、手动近似计算、数学公式法、几何
- 上一篇: 蚂蚁庄园解析:丑橘与耙耙柑是否为同种水果?
- 下一篇: 你了解吗?SSID到底是什么意思?
游戏攻略帮助你
更多+-
04/14
-
04/14
-
04/14
-
04/14
-
04/14









