揭秘：曲率公式的全面解析

曲率，这一在微分几何中占据核心地位的概念，描述了曲线在某一点处的弯曲程度。对于那些对曲率公式感兴趣的朋友来说，了解这一公式不仅能够帮助他们更好地把握曲线的几何特征，还能为他们在物理学、工程学及计算机图形学等领域的学习和研究提供有力支持。

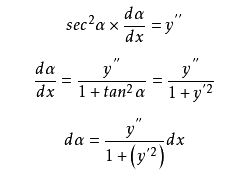
曲率的定义

在数学上，曲率是指曲线在某一点处的切线方向角对弧长的转动率，是表明曲线偏离直线程度的数值。简而言之，曲率反映了曲线在某一点处的弯曲程度。曲线的曲率越大，表示其弯曲程度越高；反之，曲率越小，曲线的弯曲程度就越低。值得注意的是，曲率半径是曲率的倒数，也就是说，曲率半径越小，曲线的弯曲程度越大。

曲率公式的推导

设曲线的直角坐标方程为y=f(x)，且y=f(x)具有二阶导数。为了求解曲线在点M处的曲率，我们需要先找到该点处切线的斜率，进而利用导数的关系推导出曲率的计算公式。

1. 切线斜率：

设曲线在点M处的切线斜率为k_1，则k_1=dy/dx=f'(x)。

2. 曲率公式：

考虑曲线在点M附近的微小变化，设弧长为Δs，切线转角为Δα。当Δs趋近于0时，Δα/Δs的极限即为曲线在点M处的曲率k。

通过一系列复杂的数学推导，我们可以得到曲率的计算公式为：

k = |y''/[(1+(y')^2)^(3/2)]|

其中，y'和y''分别为函数y对x的一阶和二阶导数。

参数方程下的曲率公式

在实际应用中，许多曲线并不能直接表示为y=f(x)的形式，而是需要通过参数方程来描述。设曲线的参数方程为r(t)=(x(t),y(t))，其中t为参数。此时，我们可以利用参数方程求导法来求解曲率。

1. 一阶导数：

x'=dx/dt，y'=dy/dt

2. 二阶导数：

x''=d^2x/dt^2，y''=d^2y/dt^2

3. 曲率公式：

在参数方程下，曲率的计算公式为：

k = |(x'y'' - x''y')/((x')^2 + (y')^2)^(3/2)|

这个公式适用于平面曲线。对于三维空间中的曲线，我们可以将其视为三维向量函数r(t)=(x(t),y(t),z(t))，并利用向量的外积来求解曲率。

三维空间中的曲率公式

设三维向量函数r(t)=(x(t),y(t),z(t))，其中t为参数。此时，曲率k可以通过以下公式求解：

k = |r'×r"|/(|r'|)^(3/2)

其中，r'和r"分别为r(t)对t的一阶和二阶导数，|x|表示向量x的长度，×表示向量的外积。向量的外积定义如下：

若a=(a1,a2,a3)，b=(b1,b2,b3)，则a×b=(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)。

曲率的性质和应用

曲率作为一种重要的几何量，在微分几何、物理学、工程学和计算机图形学等领域都有着广泛的应用。

1. 几何特征描述：

曲率可以用来描述曲线的几何特征，如弯曲程度、拐角和尖锐程度等。通过计算曲率，我们可以判断曲线的凹凸性、拐点位置以及曲线的整体形状。

2. 物理学应用：

在物理学中，曲率常用于描述物理场的弯曲程度，如引力场中的时空弯曲。爱因斯坦的广义相对论就利用了曲率来描述时空的几何结构。

3. 工程学应用：

在工程学中，曲率被广泛应用于道路设计、桥梁结构、飞机和汽车的外形设计等领域。通过合理设计曲线的曲率，可以提高结构的稳定性和安全性。

4. 计算机图形学应用：

在计算机图形学中，曲率被用于三维模型的渲染、平滑处理和纹理映射等方面。通过计算曲率，我们可以生成更加真实和细腻的三维效果。

曲率半径和曲率圆

曲率半径是曲率的倒数，它表示了曲线在某一点处附近圆弧的半径。曲