向量平行与垂直的公式详解

向量，这一数学概念，在现代数学、物理学以及工程学中扮演着举足轻重的角色。无论是在解析几何的精确描绘中，还是在物理力学的深入剖析里，向量都以其独特的性质和运算规则，为我们提供了一种直观而强大的工具。而在向量的诸多性质中，平行与垂直无疑是最为基础和重要的两个概念。它们不仅决定了向量之间的空间关系，还是解决许多实际问题时不可或缺的关键。那么，向量平行与垂直的公式是什么呢？让我们一起揭开它们的神秘面纱。

首先，我们需要明确向量的基本概念。向量，简而言之，就是一个既有大小又有方向的量。在数学上，一个向量通常用一个带有箭头的线段来表示，线段的长度代表向量的大小，箭头的方向则代表向量的方向。而在二维或三维坐标系中，向量还可以通过坐标来表示，例如，一个二维向量a可以表示为(a1, a2)，其中a1和a2分别是向量a在x轴和y轴上的分量。

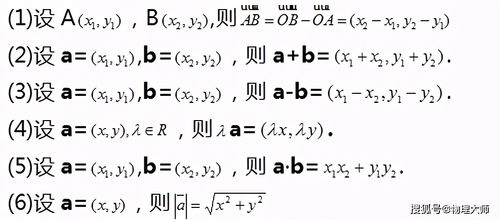
接下来，我们来看向量平行的公式。如果两个向量a和b平行（或称为共线），那么它们之间必然存在一个非零实数k，使得a = kb。这个公式揭示了向量平行的本质：一个向量可以通过另一个向量乘以一个常数来得到。换句话说，两个平行的向量在同一直线上，只是大小和方向（或反方向）可能有所不同。在坐标表示下，如果向量a = (a1, a2)，向量b = (b1, b2)，且a与b平行，那么必然存在k ≠ 0，使得a1 = kb1且a2 = kb2。从这个等式中，我们可以推导出向量平行的另一个条件：两向量的对应分量之比相等，即a1/b1 = a2/b2（注意，这里要求b1和b2都不为零，以避免分母为零的情况）。这个条件在判断两个向量是否平行时非常实用。

然而，仅仅知道向量平行的公式是不够的。在很多实际问题中，我们还需要判断向量是否垂直。向量垂直的概念同样重要，因为它决定了两个向量在空间中的正交关系。在二维平面上，如果两个向量垂直，那么它们之间的夹角就是90度；在三维空间中，这个概念同样适用，只是夹角需要在三个坐标平面上分别考虑。

那么，向量垂直的公式是什么呢？对于两个二维向量a = (a1, a2)和b = (b1, b2)，如果它们垂直，那么它们的点积（也称为内积或数量积）必然为零。点积的定义是：a · b = a1b1 + a2b2。因此，向量a和b垂直的条件就是a1b1 + a2b2 = 0。这个公式非常简洁明了，只需将两个向量的对应分量相乘后相加，如果结果为零，则两个向量垂直。

值得注意的是，向量垂直的条件在三维空间中同样适用。对于两个三维向量a = (a1, a2, a3)和b = (b1, b2, b3)，如果它们垂直，那么它们的点积也必须为零，即a1b1 + a2b2 + a3b3 = 0。这个公式在三维空间中判断向量垂直时同样有效。

此外，向量垂直还有一些其他的性质。例如，在二维平面上，如果两个向量垂直，那么它们的方向向量之间的夹角就是90度或270度（即相差π/2弧度）。在三维空间中，这个性质同样成立，只是夹角需要在三个坐标平面上分别考虑。另外，如果两个向量都垂直于同一个向量（称为法向量），那么这两个向量也必然平行（或在三维空间中可能共面但不同向）。这个性质在向量空间中的几何关系分析中非常有用。

在实际应用中，向量平行与垂直的公式和性质有着广泛的应用。例如，在物理学中，力、速度和加速度等物理量都是向量。当这些物理量平行或垂直时，它们的相互作用和效果会有很大的不同。在工程学中，向量的平行与垂直关系也常用于结构设计、运动分析和信号处理等领域。在解析几何中，向量的平行与垂直更是解决许多几何问题的基础和关键。

综上所述，向量平行与垂直的公式和性质是向量理论中不可或缺的重要组成部分。它们不仅揭示了向量之间的空间关系，还为解决许多实际问题提供了有力的数学工具。通过学习和掌握这些公式和性质，我们可以更加深入地理解和应用向量的概念和方法，从而在数学、物理学和工程学等领域中取得更加丰硕的成果。

对于那些对向量平行垂直公式感兴趣的用户来说，了解这些公式和性质只是第一步。接下来，他们还需要通过大量的练习和实践来加深对这些概念的理解和掌握。在这个过程中，他们可能会遇到各种各样的问题和挑战，但正是这些挑战才促使他们不断进步和提高。因此，建议那些对向量平行垂直公式感兴趣的用户不要止步于此，而是继续深入学习和探索这个充满魅力和挑战的数学领域。