揭秘抛物线方程的奥秘

在数学的广阔领域中，抛物线方程占据着举足轻重的地位。它不仅在几何学中是描述抛物线形状的数学表达式，而且在物理学、工程学乃至经济学等多个学科中都有广泛的应用。本文将围绕抛物线方程的基本概念、标准形式、性质、推导方法以及实际应用等方面展开探讨，带您深入了解这一数学瑰宝。

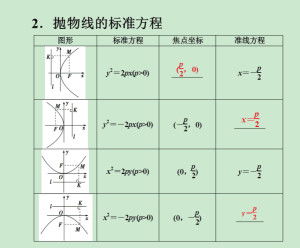
首先，我们来明确一下什么是抛物线。抛物线是一种平面曲线，其上任一点到一条固定直线（称为准线）和到一个固定点（称为焦点）的距离相等。这种独特的性质使得抛物线在视觉上呈现出一种优雅的对称美。而抛物线方程，则是用来精确描述这种曲线形状的数学工具。

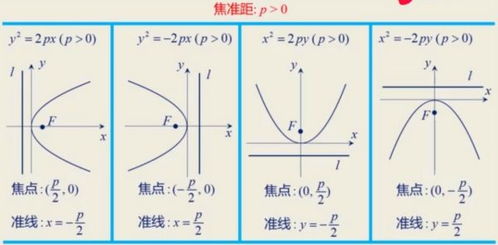
抛物线方程的标准形式有多种，其中最常见的是开口向上或向下的抛物线方程y=ax²+bx+c（a≠0）。在这个方程中，a、b、c是常数，它们决定了抛物线的具体位置和形状。特别是，a的值决定了抛物线的开口方向和大小：当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。而|a|的值越大，抛物线的开口就越窄；|a|的值越小，抛物线的开口就越宽。b和c的值则影响抛物线的水平和垂直位置。

除了上述标准形式外，抛物线方程还可以表示为其他形式，以适应不同的应用场景。例如，当抛物线的顶点不在原点时，我们可以使用顶点式y=a(x-h)²+k来描述它，其中(h,k)是抛物线的顶点坐标。这种形式直接揭示了抛物线的顶点位置，使得在计算和作图时更加便捷。

接下来，我们探讨一下抛物线的一些基本性质。首先，抛物线是轴对称图形，其对称轴是直线x=h（在顶点式中）。这意味着，如果我们在抛物线上找到一点P(x,y)，那么它的对称点P'(2h-x,y)也必定在抛物线上。其次，抛物线有一个顶点，它是抛物线上最低（或最高）的点，其坐标为(h,k)。此外，抛物线还与x轴有一个或两个交点（称为抛物线的根），这些交点的x坐标是方程ax²+bx+c=0的解。

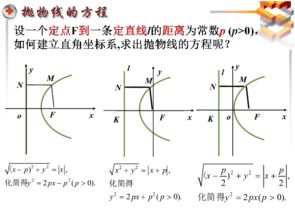
那么，如何推导出抛物线方程呢？这通常涉及到一些几何和代数的知识。以开口向上的抛物线为例，我们可以从焦点和准线的定义出发，利用点到直线的距离公式和点到点的距离公式，建立一个关于x和y的等式。然后，通过化简和整理，我们就可以得到一个形如y=ax²+bx+c的抛物线方程。同样地，对于开口向下、向左或向右的抛物线，我们也可以采用类似的方法来推导其方程。

在实际应用中，抛物线方程的应用范围非常广泛。在物理学中，抛物线方程被用来描述抛体运动（如投掷、射击等）的轨迹。通过求解抛物线方程，我们可以预测物体在不同时间点的位置和速度，从而为运动训练和工程设计提供重要参考。在工程中，抛物线方程也被广泛应用于桥梁、拱门等结构的设计中。这些结构通常呈现出抛物线的形状，以承受来自上方的压力和下方的拉力。通过精确计算抛物线方程的参数，工程师可以确保结构的稳定性和安全性。

此外，抛物线方程还在经济学和金融学中有重要应用。例如，在投资组合管理中，投资者通常会利用抛物线方程来描述不同资产之间的风险-收益关系。通过求解这个方程，投资者可以找到最优的投资组合配置，以实现风险和收益之间的最佳平衡。

当然，抛物线方程的学习和应用并不仅仅局限于上述领域。在数学教育中，抛物线方程是一个重要的教学内容。通过学习抛物线方程的概念、性质和推导方法，学生可以培养自己的逻辑思维能力和空间想象能力。同时，抛物线方程也是数学竞赛和高考数学中的重要考点之一。因此，对于广大数学爱好者和学生来说，深入理解和掌握抛物线方程的知识是至关重要的。

值得注意的是，虽然抛物线方程在数学和物理学等领域中有着重要的应用价值，但在实际应用中我们也需要注意其局限性和适用性。例如，在描述抛体运动时，抛物线方程只适用于空气阻力可以忽略不计的情况。当空气阻力较大时，物体的运动轨迹将不再呈现抛物线形状。因此，在使用抛物线方程进行预测和计算时，我们需要根据具体情况进行合理的假设和近似处理。

综上所述，抛物线方程作为一种重要的数学工具，在多个学科和领域中都有着广泛的应用。通过深入学习和理解抛物线方程的概念、性质和推导方法，我们可以更好地应用这一数学工具来解决实际问题。同时，我们也需要注意其局限性和适用性，以确保在实际应用中的准确性和可靠性。在未来的学习和工作中，让我们继续探索和学习更多的数学知识，为人类的科技进步和社会发展贡献自己的力量。