如何计算圆的周长

圆的周长，这一几何学中的基础概念，自古以来便吸引着无数数学家和学者的目光。它不仅是日常生活中常见的形状特征，更是数学理论研究和实际应用的基石。在深入探讨如何计算圆的周长之前，我们首先需要明确几个关键词：圆、直径、半径、π（圆周率）以及周长公式。

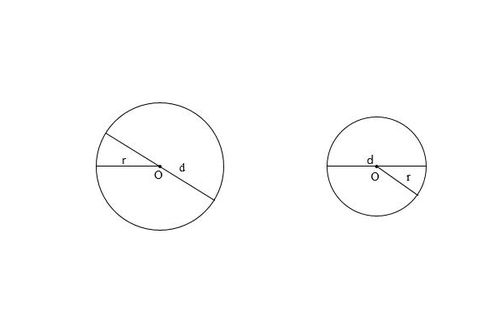
圆，作为一种平面几何图形，定义为所有与给定点（称为圆心）距离相等的点的集合。这个相等的距离，我们称之为半径，记作r。而直径则是穿过圆心、两端点均在圆上的线段，其长度是半径的两倍，记作d（d=2r）。

圆周率π，是一个无理数，它在圆的周长与直径之间的关系中扮演着至关重要的角色。简单来说，π是圆的周长与其直径的比值，即C/d=π，其中C代表圆的周长。这个比值对于任何圆都是恒定的，不随圆的大小而改变。π的值约为3.14159...，尽管人们已经计算出了它的数十亿位小数，但它的小数部分永远不会终止也不会循环，这使其成为了数学中的一个神秘而迷人的常数。

接下来，我们重点关注如何计算圆的周长。历史上，许多伟大的数学家都为求解这一问题付出了巨大的努力。早在古希腊时期，数学家阿基米德就通过近似多边形逼近圆的方法，估算出了π的值，从而间接地得出了圆的周长计算公式。时至今日，我们已经拥有了精确而简洁的圆的周长公式：C=2πr或C=πd。这两个公式是等价的，可以根据已知条件（半径或直径）直接计算出圆的周长。

在实际应用中，这两个公式具有广泛的适用性。例如，在建筑设计中，我们可能需要计算圆形柱子的周长以确定所需的装饰材料；在物理学中，了解圆的周长有助于我们计算圆周运动中的速度和加速度；在电子工程中，圆的周长与电路板的布局设计密切相关。

然而，值得注意的是，虽然圆周长的计算公式看似简单，但在实际计算中，由于π是一个无理数，我们无法得到一个精确到有限位数的结果。因此，在实际应用中，我们通常会根据需要选择π的近似值进行计算。例如，对于日常计算，我们可以使用3.14作为π的近似值；而在需要更高精度的场合，则可以使用更多的位数来表示π。

此外，随着计算机科学的发展，我们可以利用编程语言和数学软件来计算圆的周长，从而得到更高精度的结果。这些工具不仅提供了高效的数值计算能力，还允许我们进行复杂的数学分析和模拟实验。

除了基本的周长计算外，圆的周长还与一些有趣的数学问题和现象紧密相连。例如，著名的“化圆为方”问题就是一个古老的几何难题，它要求使用有限次的直尺和圆规作图来构造一个与给定圆面积相等的正方形。虽然这个问题在古希腊时期就被提出，但直到19世纪才被数学家们证明为不可解。在这个过程中，圆的周长和面积的计算成为了探讨这一问题的关键。

另一个与圆的周长相关的有趣现象是“黄金分割”。黄金分割是一种在自然界和艺术作品中广泛存在的比例关系，它可以用圆的周长和半径来构造。具体来说，如果我们画一个圆，并在圆内画一个正六边形，那么连接正六边形的每个顶点与圆心的线段就会将圆分割成六个等边三角形。此时，如果我们延长这些线段直到它们与圆相交于另一点，那么这些交点与圆心之间的线段就会将圆分割成两个面积相等的部分。而这两个部分的比值（较长部分与较短部分的比值）就是黄金分割比。这一发现不仅揭示了圆的周长与自然界中某些美学规律的关联，还为数学和艺术之间的桥梁增添了新的维度。

此外，圆的周长还与一些重要的数学定理和公式紧密相连。例如，欧拉公式e^(iπ)+1=0将数学中的五个基本常数（自然对数的底e、虚数单位i、圆周率π、1和0）巧妙地结合在一起，展示了它们之间的深刻联系。这一公式不仅在复变函数论和解析数论中具有重要的应用价值，还激发了数学家们对自然界和数学中和谐统一之美的无限遐想。

综上所述，圆的周长作为几何学中的一个基本概念，不仅具有广泛的应用价值，还蕴含着丰富的数学内涵和美学意义。通过深入了解和探索圆的周长及其相关性质，我们可以更好地理解自然界的规律、欣赏数学中的和谐之美以及推动科学技术的进步。因此，无论是在学术研究还是实际应用中，圆的周长都值得我们深入研究和不断探索。