取整函数是如何进行取整的？

在数学的广阔领域中，取整函数是一个既基础又实用的工具。它能够将一个实数映射到一个最接近的整数，这在计算机编程、统计分析、物理计算等多个领域都发挥着至关重要的作用。本文将详细探讨取整函数的原理、常见的取整方法及其应用场景，旨在帮助读者全面理解“取整函数怎么取整”。

一、取整函数的基本概念

取整函数，简而言之，是将一个实数转换为最接近的整数的数学工具。在计算机科学中，这种转换被称为“舍入”或“取整”。需要注意的是，取整并不是简单的四舍五入，实际上有多种不同的规则来决定如何将一个实数映射到整数上。

二、常见的取整方法

1. 向下取整（Floor Function）

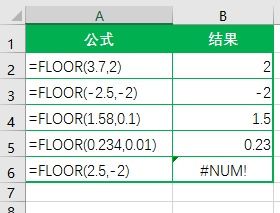
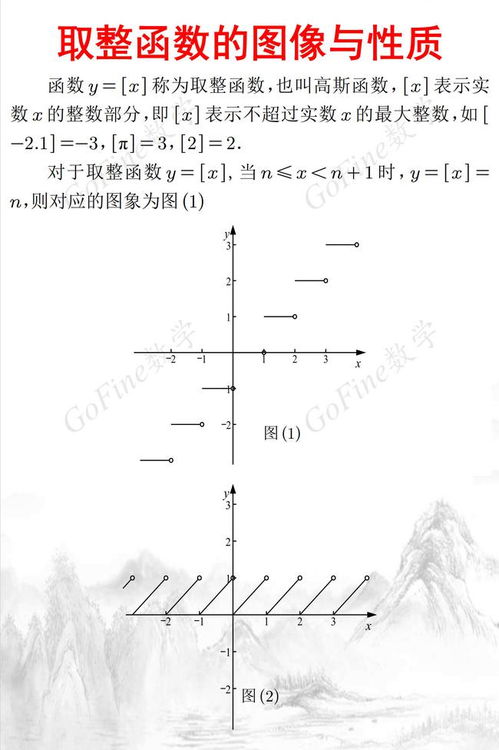
向下取整函数通常表示为floor(x)，其中x是待取整的实数。这个函数会将x映射到小于或等于x的最大整数。例如，floor(3.7)的结果是3，floor(-2.3)的结果是-3。在数轴上，可以想象一个向下“砍”的动作，即将所有小数部分“砍掉”，只保留整数部分。

2. 向上取整（Ceiling Function）

与向下取整相反，向上取整函数表示为ceil(x)，它将x映射到大于或等于x的最小整数。例如，ceil(3.2)的结果是4，ceil(-2.8)的结果是-2。在数轴上，这个动作就像是向上“托”起，使得结果总是比原数大或相等（如果原数本身就是整数）。

3. 四舍五入（Rounding Function）

四舍五入是日常生活中最常用的取整方法之一，其函数表示为round(x)。它根据x的小数部分是否大于等于0.5来决定向上还是向下取整。例如，round(3.5)的结果是4，round(2.4)的结果是2。当x的小数部分恰好为0.5时，大多数编程语言和数学标准规定，四舍五入到最接近的偶数整数（这种规则被称为“银行家舍入”，因为它能减少因舍入产生的累计误差）。

4. 截断（Truncation）

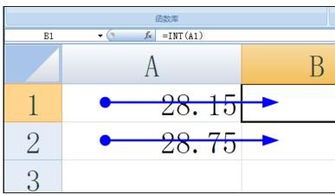
截断取整直接丢弃x的小数部分，保留整数部分，而不考虑小数部分的大小。这种行为在编程中通常通过类型转换（如将浮点数转换为整数）来实现。例如，截断3.9的结果是3，截断-2.1的结果也是-2。与向下取整不同，截断不关心被截断的数是否小于原数（在负数情况下会有所不同）。

5. 向零取整（Towards Zero Rounding）

向零取整，有时也称为“截断式取整”，其实质是总是朝着零的方向取整。正数的行为与截断相同，负数的行为与向下取整相同。例如，向零取整3.7的结果是3，而向零取整-3.7的结果是-3。

三、取整方法的数学表达与性质

对于上述每种取整方法，都可以通过数学表达式来定义它们的性质。例如，对于任意实数x：

floor(x) ≤ x < floor(x) + 1

ceil(x) - 1 < x ≤ ceil(x)

当0.5 ≤ |x - round(x)| < 0.5时，round(x)按照银行家舍入规则决定

trunc(x)的整数部分等于x的整数部分，不考虑符号

towardsZeroRound(x)的行为根据x的符号分别类似于floor(x)（x为正）或ceil(x)（x为负）

四、取整函数的应用场景

1. 计算机编程

在编程中，取整函数常用于类型转换、数组索引计算、图形处理等领域。例如，在计算屏幕上像素位置时，通常需要将浮点数坐标转换为整数坐标。

2. 统计分析

在统计分析中，数据往往需要先进行标准化处理，如将连续变量离散化为分类变量。此时，取整函数（尤其是四舍五入）可以用来定义分类的边界。

3. 物理计算

在物理学中，尤其是在模拟连续系统时（如流体动力学模拟），为了简化计算，常需要将连续变量（如速度、压力）离散化为整数网格点上的值。

4. 金融学

在金融领域，尤其是在利率计算和货币兑换中，四舍五入和银行家舍入的应用非常广泛，以确保计算的公平性和准确性。

5. 计算机科学中的图形渲染

在3D图形渲染中，为了处理纹理映射、光照计算等，需要将浮点坐标转换为整数坐标以访问像素数据。这时，通常会用到截断或向下取整。

五、取整函数的注意事项

精度损失：在使用取整函数时，需要