rad与deg的换算方法

在数学、物理以及工程学中，角度的度量是一个基础且重要的概念。我们经常需要用到两种主要的角度单位：弧度（rad）和度数（deg）。尽管它们都是用来描述一个角的大小，但它们的定义和应用场景却有所不同。本文将从多个维度探讨弧度与度数之间的换算，以及它们在各个领域中的实际应用。

一、定义与基础

度数（deg）

度数是我们日常生活中最常见的角度度量单位。一个完整的圆被分成360等份，每一份即为1度。当我们说一个直角是90度时，意味着这个角占据了圆的四分之一。度数单位适合在几何学、天文学和一些基本的物理计算中使用，因为它符合我们的直觉和日常经验。

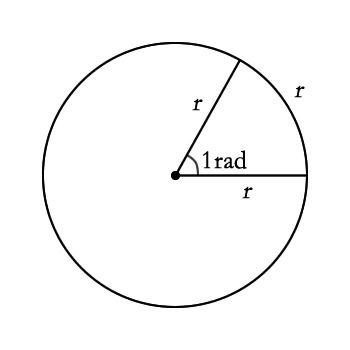
弧度（rad）

弧度则是基于圆的半径来定义的。一个完整的圆对应的弧度值为2π（π约为3.14159...）。弧度制的核心在于它与圆的弧长与半径之间的关系。具体来说，如果一个弧长等于圆的半径，那么这个弧对应的角度就是1弧度。弧度制在计算三角函数、积分、微分方程等领域中更加便利，因为它直接与圆的几何属性相关联。

二、换算公式

弧度与度数之间的换算公式是：

\[ \text{度数} = \left( \frac{180}{\pi} \right) \times \text{弧度} \]

\[ \text{弧度} = \left( \frac{\pi}{180} \right) \times \text{度数} \]

这两个公式帮助我们在这两个角度单位之间快速转换。例如，如果我们想知道90度等于多少弧度，我们可以使用第二个公式计算得到π/2弧度。反过来，如果我们想知道π弧度对应的度数，使用第一个公式就可以得到180度。

三、三角函数中的应用

三角函数，如正弦（sin）、余弦（cos）和正切（tan），在物理学、工程学以及数学分析中占据核心地位。在弧度制下，这些函数的性质更易于理解和应用。例如，正弦函数sin(x)在x=π/2时达到最大值1，这对应于一个直角。在度数制下，我们则需要记住sin(90°)=1，但弧度制与圆的弧长和半径之间的直接关联使得这一性质更加直观。

此外，在微积分中，弧度制的使用也是不可或缺的。当我们在求解涉及三角函数的导数或积分时，弧度制可以简化计算过程，因为它允许我们直接利用圆的几何性质。

四、物理与工程中的应用

在物理学和工程学中，角度单位的选择往往取决于具体问题的性质和计算的需求。例如，在力学和动力学分析中，当涉及到旋转运动和角速度时，弧度制通常更为方便。角速度的定义是单位时间内角度的变化量，在弧度制下，它直接对应于弧长与时间的比值，这与线速度的定义（单位时间内位移的变化量）保持一致。

在电气工程中，相位角的概念也是基于弧度制的。交流电（AC）的相位角描述了电流和电压波形之间的时间偏移，这个偏移量通常以弧度表示。使用弧度制可以更直接地应用欧拉公式（e^(ix)=cos(x)+isin(x)），它在电路分析和信号处理中非常重要。

五、几何学与天文学的应用

在几何学中，尽管度数制更为直观和常用，但在某些情况下，弧度制也提供了便利。例如，在求解涉及圆的几何问题时，弧度制可以更简洁地表示弧长和角度之间的关系。此外，弧度制在解析几何和微分几何中也扮演着重要角色，它使得曲线的参数化和曲率的计算更加直观。

天文学中，尽管我们通常使用度数来描述恒星和行星的位置，但在某些高级计算中，弧度制也是必不可少的。例如，在计算行星轨道的摄动时，使用弧度制可以更精确地描述轨道的变化。

六、编程与计算机科学中的应用

在编程和计算机科学中，角度单位的选择通常取决于具体的应用场景和库函数的设计。许多编程语言和数学库都提供了处理弧度和度数的函数。例如，在Python的math库中，三角函数如sin()、cos()和tan()默认接受弧度作为输入。如果需要使用度数，则需要通过额外的转换步骤，或者使用专门的函数（如math.radians()和math.degrees()）进行单位转换。

在图形学、游戏开发和虚拟现实等领域中，角度单位的选择也取决于具体的需求。例如，在渲染三维场景时，弧度制通常用于描述旋转和视角的变化，因为它与圆的几何属性直接相关。而在用户界面设计中，度数制可能更易于用户理解和操作。

七、教育与实践中的考量

在教育领域，角度单位的转换通常是一个基本的数学教学内容。学生需要理解弧度制和度数制的定义、换算方法以及它们在不同领域中的应用。通过实践练习和案例分析，学生可以逐渐掌握这些概念，并在实际问题解决