斜二测画法详细步骤指南

斜二测画法是绘制空间几何直观图的一种重要且实用的方法，它能够帮助我们将三维空间中的图形以富有立体感且易于理解的方式呈现在二维平面上。这种方法不仅能够准确地表达出图形各主要部分的位置关系，还能保持良好的度量关系，使图形的空间感得以体现。接下来，我们将详细介绍斜二测画法的步骤，确保每一步都通俗易懂。

斜二测画法的基本步骤

1. 建立平面直角坐标系

首先，我们需要在已知的平面图形中确定两个互相垂直的轴，通常取为x轴和y轴，它们相交于点O。这个步骤相当于为图形设定一个基准框架，便于后续的转换和绘制。

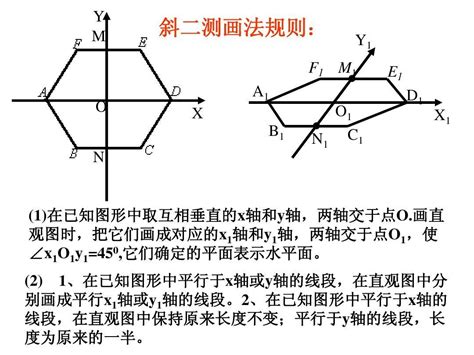
2. 画出斜坐标系

接下来，我们在绘制直观图的纸上（或者说平面上）画出对应的x'轴和y'轴，这两轴相交于点O'。这里的关键是使∠x'O'y'等于45°（或135°），这个角度的设定是为了确保图形在转换后能够保持良好的立体感。这两条轴确定的平面表示水平平面，也就是我们在二维平面上模拟的三维空间中的水平面。

3. 画对应图形

在确定了斜坐标系后，我们就可以开始将原图形中的线段转换到新的坐标系中了。

平行于x轴的线段：这些线段在直观图中仍然保持平行于x'轴，并且长度不变。

平行于y轴的线段：这些线段在直观图中将变为平行于y'轴，但长度变为原来的一半。

对于一般的线段，我们需要在原图形中从线段的各个端点引垂线，然后按照上述规则画出这些线段，确定它们的端点，最终连接起来。这一步骤可能需要一些细致的计算和绘制，但一旦掌握了方法，就会变得相对简单。

4. 连接线段并确定端点

在将所有需要的线段都转换到斜坐标系后，下一步就是连接这些线段的端点，形成完整的图形。这个过程中需要注意的是，要确保每一条线段都正确地连接到了它的端点，这样才能保证最终图形的准确性。

5. 擦去辅助线

在所有的线段都连接完成后，我们需要擦去x'轴、y'轴以及为了绘制图形而添加的其他辅助线。这些辅助线在绘制过程中起到了重要的作用，但在最终的图形中是不需要显示的。

实例演示：用斜二测画法画出正六边形的直观图

为了更好地理解斜二测画法的步骤，我们可以通过一个具体的例子来进行演示，这里以水平放置的正六边形为例。

第一步：建立坐标系

在六边形ABCDEF中，我们取AD所在的直线为x轴，对称轴MN所在的直线为y轴，两轴交于点O。然后，我们在纸上画出对应的x'轴和y'轴，使∠x'O'y' = 45°。

第二步：画出底面和主要线段

以O'为中心，在x'轴上取A'D' = AD，在y'轴上取M'N' = 1/2MN。接着，以点N'为中心，画出B'C'平行于x'轴，并且长度等于BC。再以点M'为中心，画出E'F'平行于x'轴，并且长度等于EF。

第三步：连接线段并确定形状

接下来，我们连接A'B'、A'F'、A'D'、C'D'，并擦去辅助线x'轴和y'轴。这样，我们就得到了正六边形ABCDEF水平放置的直观图A'B'C'D'E'F'。

斜二测画法的应用与注意事项

斜二测画法不仅适用于平面图形的绘制，还可以用于绘制三维几何体的直观图。在绘制三维几何体的直观图时，步骤稍有不同，但基本原理是相同的。

画三维几何体直观图的一般步骤：

1. 画轴：画出x、y、z三轴交于原点，使xOy = 45°、xOz = 90°。

2. 画底面：在相应轴上取底面的边，并交于底面各顶点。

3. 画侧棱或横截面侧边：使其平行于z轴。

4. 成图：连接相应端点，去掉辅助线，将被遮挡部分改为虚线等。

在绘制三维几何体的直观图时，如果不作严格要求，图形尺寸可以适当选取。用斜二测画法画图的角度也可以是自定的，但要求图形有一定的立体感。

注意事项：

在绘制过程中，要确保每一条线段都正确地连接到了它的端点。

在转换线段时，要注意平行于x轴的线段长度不变，平行于y轴的线段长度