轻松学会：如何计算正方体的体积

正方体体积的计算是几何学中的一个基础而重要的知识点。无论是在日常生活、工程设计还是科学研究中，了解如何准确计算正方体的体积都显得尤为重要。本文将从正方体的定义、性质出发，详细讲解正方体体积的计算方法，并通过实例加深理解，使读者能够全面掌握这一知识点。

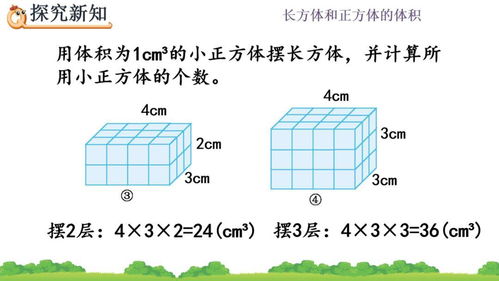
正方体，作为一种特殊的立体几何图形，其六个面均为正方形，且所有棱长相等。这一特性使得正方体在几何学中占据了独特地位。为了深入理解正方体体积的计算方法，我们首先需要明确正方体的几个关键性质：

1. 正方体的所有棱长相等，记作a。

2. 正方体的六个面都是正方形，且面积均为a²。

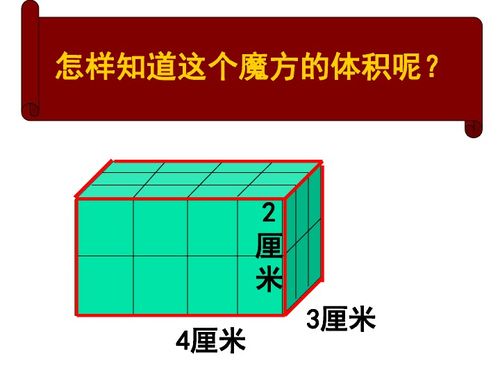
3. 正方体的体对角线长度为√3a，但这与体积计算无直接关系，仅作为正方体性质的一部分进行介绍。

接下来，我们进入正方体体积计算的核心部分。正方体体积的计算公式为：V = a³，其中V代表体积，a代表正方体的棱长。这一公式的推导基于正方体的几何特性和空间填充原理。我们可以将正方体视为由无数个边长为a的小正方体组成，每个小正方体的体积为a³，而大正方体则是由这些小正方体紧密排列而成。因此，大正方体的体积即为所有小正方体体积的总和，也即a³。

为了更直观地理解正方体体积的计算方法，我们可以通过以下步骤进行演示：

第一步，想象一个边长为a的正方体，其六个面均为正方形。

第二步，将这个正方体切割成若干个小正方体，每个小正方体的棱长同样为a。由于正方体的所有棱长相等，因此可以确保切割后的小正方体大小一致。

第三步，计算每个小正方体的体积。由于每个小正方体的棱长为a，因此其体积为a³。

第四步，将大正方体内所有小正方体的体积相加。由于大正方体是由这些小正方体紧密排列而成，因此其体积即为所有小正方体体积的总和。由于每个小正方体的体积都是a³，且数量与正方体的体积成正比（实际上，数量就是a³个，因为每个维度上都可以分割成a个小正方体），因此大正方体的体积也就是a³个小正方体的体积之和，即V = a³。

通过以上步骤，我们可以清晰地看到正方体体积计算公式的由来。这一公式不仅简洁明了，而且具有广泛的应用价值。

在实际应用中，正方体体积的计算方法可以用于解决多种问题。例如，在建筑设计中，我们需要计算房间的体积以确定所需的材料数量和成本；在物理学中，了解正方体的体积有助于我们计算物体的质量、密度等物理量；在日常生活中，我们也经常需要用到正方体体积的计算方法，如计算储物箱、冰箱等容器的容量。

此外，正方体体积的计算还可以与其他几何知识相结合，解决更复杂的问题。例如，我们可以将正方体切割成多个小正方体或长方体，然后分别计算它们的体积并求和，以得到原正方体的体积。这种方法虽然繁琐，但在某些特定情况下可能更为实用。

为了加深对正方体体积计算方法的理解，我们可以看一个具体的例子：

假设有一个边长为3米的正方体房间，我们需要计算这个房间的体积。根据正方体体积的计算公式V = a³，我们可以将a替换为3米，得到V = 3³ = 27立方米。因此，这个房间的体积为27立方米。

通过这个例子，我们可以看到正方体体积的计算方法在实际应用中的具体运用。同时，这个例子也展示了正方体体积计算公式在解决实际问题时的简便性和准确性。

除了正方体体积的计算方法外，我们还可以进一步探讨正方体与其他几何图形之间的关系。例如，正方体可以看作是长方体的一个特例（当长方体的长、宽、高相等时即为正方体）。因此，我们可以利用长方体的体积计算公式（V = 长 × 宽 × 高）来推导正方体的体积计算公式。当长方体的长、宽、高均为a时，其体积即为a × a × a = a³，这与我们之前得到的正方体体积计算公式是一致的。

此外，正方体还可以与其他几何图形进行组合或切割，形成更复杂的几何体。在这些情况下，我们可以通过分别计算各个部分的体积并求和或相减来得到整体几何体的体积。这种方法虽然需要一定的几何知识和计算能力，但在解决复杂问题时具有重要的作用。

综上所述，正方体体积的计算方法是几何学中的一个基础而重要的知识点。通过了解正方体的定义、性质以及体积计算公式的推导过程和应用实例，我们可以更加全面地掌握这一知识点，并在实际应用中灵活运用。无论是在日常生活、工程设计还是科学研究中，正方体体积的计算方法都发挥着重要的作用。因此，我们应该重视这一知识点的学习和掌握，以便更好地应对各种实际问题。