揭秘正方体体积的神奇计算公式！

正方体体积的计算公式是几何学中的一个基本概念，对于很多初学者和数学爱好者来说，了解并掌握这一公式是非常重要的。正方体作为一种特殊的立体图形，它的每个面都是一个正方形，且所有的棱长都相等。这一特性使得正方体在很多实际问题中都有着广泛的应用，比如建筑设计、工程计算、物理模型等。

要计算正方体的体积，首先需要明确正方体的基本特征。正方体的六个面都是正方形，每个面的面积相等，所有棱的长度也相等。假设正方体的棱长为a，那么每一个面的面积就是a的平方（a²）。这个面积公式是计算正方体表面积的基础，但对于体积的计算，我们还需要用到另一个公式。

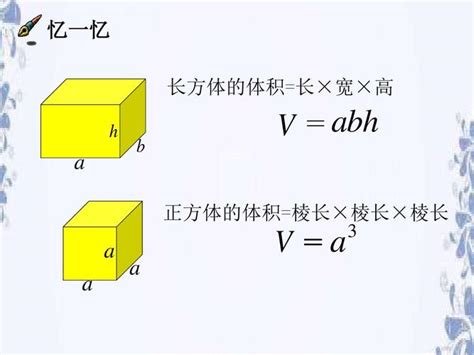
正方体体积的计算公式是：V = a³。这里，V代表正方体的体积，a代表正方体的棱长。这个公式简洁明了，却蕴含着丰富的几何意义。它告诉我们，正方体的体积与棱长的三次方成正比。也就是说，如果正方体的棱长增加一倍，那么它的体积将增加八倍。这种立方关系在几何学和物理学中都有着广泛的应用。

为了更好地理解这个公式，我们可以通过一个简单的例子来说明。假设有一个棱长为2厘米的正方体，那么它的体积就是2的三次方，即8立方厘米。如果我们把这个正方体的棱长增加到4厘米，那么它的体积就变成了4的三次方，即64立方厘米。可以看出，随着棱长的增加，正方体的体积迅速增大。

这个公式不仅适用于棱长固定的正方体，还适用于那些棱长可以变化的情况。比如，在建筑设计中，我们经常需要计算不同尺寸的正方体体积，以便选择合适的建筑材料和设计方案。通过调整正方体的棱长，我们可以得到不同体积的正方体，从而满足不同的建筑需求。

除了在建筑设计中的应用，正方体体积的计算公式还在工程计算中发挥着重要作用。在工程领域，我们经常需要计算各种形状和尺寸的立体图形的体积，以便进行材料采购、成本控制和工艺优化。正方体作为一种常见的立体图形，其体积的计算公式在工程计算中得到了广泛应用。

此外，正方体体积的计算公式还在物理学中有着广泛的应用。在物理学中，我们经常需要计算物体的质量、密度和体积等物理量。通过测量物体的棱长和计算其体积，我们可以进一步求出物体的密度和质量等物理量。这对于理解物体的物理性质和进行物理实验都非常重要。

在学习正方体体积的计算公式时，我们还需要注意一些相关的知识点。比如，正方体的表面积计算公式是6a²，这个公式与体积公式不同，但同样重要。通过比较这两个公式，我们可以发现正方体的体积与表面积之间的关系。另外，我们还需要了解正方体的其他性质，比如正方体的对角线长度、正方体的内切球和外接球等。这些性质不仅有助于我们更深入地理解正方体，还能帮助我们在实际问题中更好地应用正方体的相关公式。

为了加深对正方体体积计算公式的理解，我们可以通过一些练习题来巩固所学知识。比如，给出一个正方体的棱长，要求计算其体积；或者给出一个正方体的体积，要求求出其棱长。这些练习题不仅有助于我们掌握计算方法，还能提高我们的计算能力和解题技巧。

此外，我们还可以通过一些实际的制作活动来加深对正方体体积公式的理解。比如，我们可以动手制作一个正方体模型，并用尺子测量其棱长。然后，我们可以根据公式计算出模型的体积，并与实际测量结果进行比较。通过这种实践活动，我们可以更加直观地感受到正方体体积公式的实际应用和准确性。

总之，正方体体积的计算公式是几何学中的一个基本概念，对于很多初学者和数学爱好者来说都非常重要。通过掌握这个公式，我们可以更好地理解和应用正方体相关的知识，解决实际问题。同时，我们还可以通过这个公式拓展到其他立体图形的体积计算，进一步拓宽我们的知识面和应用能力。因此，我们应该认真学习并掌握正方体体积的计算公式，以便在未来的学习和工作中更好地应用它。