算术平方根与平方根:区别何在?
在我们探索数学的奥秘时,常常会遇到一些看似相似却又截然不同的概念。今天,我们就来揭开两个常在数学课堂上出现的术语——算术平方根和平方根之间的神秘面纱。它们之间到底有什么微妙的区别?为什么在数学学习中准确理解这些区别如此重要?让我们一起踏上这场充满智慧与发现的旅程。

首先,让我们从定义入手。平方根,简而言之,就是一个数能被哪个数的平方等于它。换句话说,如果a的平方等于b,那么a就是b的平方根。这里的关键在于,“平方根”这个概念并不局限于正数,它还包含了负数的情况。然而,当我们谈论“算术平方根”时,我们通常指的是非负的那个平方根。这是两者之间的第一个重要区别:平方根可以是正数也可以是负数,但算术平方根特指非负的那个。
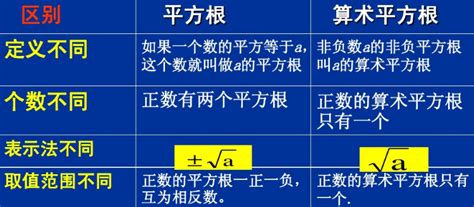
为了更好地理解这一点,让我们通过一个简单的例子来说明。假设我们要求9的平方根,根据平方根的定义,我们知道3的平方和-3的平方都是9。因此,9的平方根有两个,分别是3和-3。但是,如果我们问9的算术平方根是多少,答案就只有一个,那就是3。算术平方根总是指向那个非负的解。

这种区别在数学运算中尤为重要。当我们处理涉及平方根的实际问题时,比如物理学中的距离计算、工程学中的应力分析,或者是金融领域的风险评估,我们通常只关心非负的结果,因为这些情境下的负数解往往没有实际意义。例如,在计算一个物体的实际运动距离时,我们不会接受一个负值的答案,因为距离本身是一个非负的度量。这就是为什么在这些情况下,算术平方根成为了我们的首选工具。
接下来,让我们深入探讨一下这两个概念在函数图像上的表现。平方根函数,记作y=√x(这里我们特指实数范围内的非负平方根,即算术平方根的函数形式),其图像是一个开口向右的抛物线的一部分,从原点开始并向上延伸。这是因为对于每一个非负实数x,y=√x都只有一个非负值与之对应。相比之下,如果考虑完整的平方根函数,即包括正负两个解的y=±√x,其图像则会更加复杂,由两条对称的抛物线组成,一条位于x轴上方,另一条位于x轴下方,两者在原点相交。这种图形上的差异直观地展示了算术平方根与平方根在解集上的不同。
进一步地,我们来看看这两个概念在解方程中的应用。当我们面对形如x^2=a的方程时,我们需要根据a的正负情况来讨论解的存在性和数量。如果a是正数,那么方程有两个解,分别是正平方根和负平方根;如果a是0,那么方程有一个解,即0本身,因为0的平方也是0;而如果a是负数,在实数范围内,方程就没有解,因为任何实数的平方都是非负的。然而,如果我们只关注算术平方根,那么在解这类方程时,我们就会自动忽略掉负数的解,只寻找那个非负的解。这种选择性求解的策略在解决某些特定问题时非常有用,比如优化问题、几何问题等。
此外,算术平方根和平方根在编程和计算机科学中也有不同的处理方式。许多编程语言都提供了专门的函数来计算算术平方根(如Python中的`math.sqrt()`函数),这些函数通常只返回非负的结果。而如果你想要获取一个数的所有平方根(包括正负两个解),则可能需要自己编写额外的代码来实现这一功能。这种区别在处理大规模数据时尤为重要,因为它直接影响到算法的效率和结果的准确性。
在数学教育的背景下,理解算术平方根和平方根的区别也是培养学生逻辑思维和批判性思维能力的重要环节。通过区分这两个概念,学生可以更好地掌握数学中的符号语言,理解数学公式的本质含义,以及如何在不同的数学情境下做出合理的假设和推断。同时,这种区分也有助于提高学生的问题解决能力,使他们能够更加灵活地运用数学知识来解决实际问题。
总之,算术平方根和平方根虽然在表面上看似相似,但实际上它们在定义、函数图像、解方程以及编程应用等方面都存在着显著的差异。这些差异不仅丰富了数学学科的内涵,也为我们在解决实际问题时提供了更多的选择和灵活性。因此,在学习数学的过程中,我们应该努力掌握这些细微而重要的区别,以便更好地理解和运用数学知识,探索数学世界的无限魅力。
通过今天的讨论,希望你已经对算术平方根和平方根的区别有了更加清晰的认识。记住,数学是一门需要精确和严谨态度的学科,每一个细节都值得我们仔细琢磨和深入思考。在未来的数学学习中,愿你能够继续保持这份好奇心和探索精神,不断发现新的知识和方法,成为数学世界中的一名优秀探险家!
- 上一篇: 微信轻松搞定!如何查询并订购汽车票?
- 下一篇: 农业银行无卡取款操作流程指南
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/07
-
02/07
-
02/07
-
02/07
-
02/07









