揭秘：平行四边形的真正定义是什么？

探索几何之美：深入解析平行四边形的定义与魅力

在数学的浩瀚宇宙中，平行四边形如同一颗璀璨的星辰，以其独特的性质和广泛的应用，吸引着无数求知者的目光。它不仅是几何学中的基础图形，更是连接代数与几何的桥梁，承载着无数数学定理与公式。今天，让我们一起走进平行四边形的世界，深入探索它的定义、性质及其所蕴含的几何之美。

想象一下，你手中握着一张透明的纸片，轻轻对折，使两边完全重合。松开手，纸片自然展开，一个生动的平行四边形跃然眼前。这就是平行四边形最直观、最朴素的定义：两组对边分别平行的四边形。没错，就是这么简单，却蕴含着无穷的魅力。

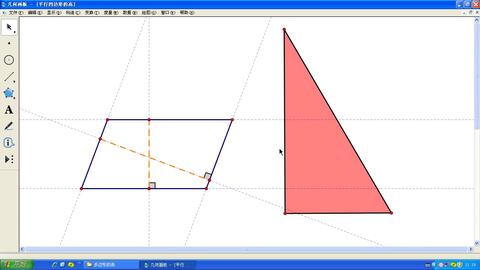
平行四边形的定义中，“平行”二字是关键。在平面几何中，平行是指两条直线在同一平面内且不相交。当这样的两条直线成为四边形的两组对边时，这个四边形就被赋予了“平行四边形”的称谓。它可以是正方形、矩形、菱形等特殊平行四边形的化身，也可以是更加自由的、形态各异的普通平行四边形。

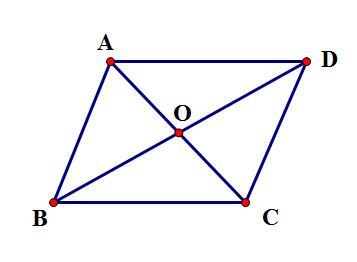
走进平行四边形的内部，你会发现更多令人着迷的性质。首先，平行四边形的对角线互相平分。这意味着，如果你用一条直线连接平行四边形的两个对角顶点，这条直线会将平行四边形分为两个面积相等的三角形。这一性质不仅美观，而且在解决实际问题时非常有用，比如在计算面积、分割图形等方面。

平行四边形的对边不仅平行，而且等长。这一性质使得平行四边形在视觉上更加和谐、统一。当你漫步在城市的街道，抬头望向那些错落有致的建筑，不难发现平行四边形元素的运用。它们或作为窗户的轮廓，或作为墙面的装饰，为城市增添了一份现代与时尚的气息。

平行四边形的角度性质同样值得探讨。在平行四边形中，同旁内角互补，即两个相邻的内角之和为180度。这一性质使得平行四边形在构图时更加灵活多变，可以创造出丰富的视觉效果。同时，它也为解决角度问题提供了便利，比如在证明角度相等、计算角度大小等方面。

在平行四边形的大家庭中，有几个特殊的成员格外引人注目。矩形，作为平行四边形的特例，它的所有内角都是直角，这使得它在建筑、工程等领域具有广泛的应用。正方形的四条边等长且四个内角都是直角，它既是矩形又是菱形，是几何图形中的“全能选手”。菱形则以其独特的对角线性质著称，它的对角线互相垂直且平分每一组对角。这些特殊的平行四边形不仅丰富了平行四边形的内涵，也为数学研究提供了更多的可能性。

平行四边形的魅力不仅仅在于其几何性质，更在于它与生活的紧密联系。在艺术创作中，平行四边形被广泛应用于绘画、雕塑等领域，成为艺术家表达创意、塑造美感的重要工具。在建筑设计中，平行四边形元素的运用使得建筑作品更加现代、时尚，成为城市天际线中一道亮丽的风景线。在科技领域，平行四边形作为图形处理、计算机视觉等技术的基础元素之一，为人工智能、虚拟现实等前沿科技的发展提供了有力支持。

此外，平行四边形在数学教育中也扮演着重要角色。它是学生接触几何知识、培养空间想象力的基础图形之一。通过学习平行四边形的性质、判定方法等内容，学生可以逐步建立起对几何图形的认知框架，为后续学习更加复杂的几何知识打下坚实的基础。

当然，平行四边形的学习并非一蹴而就。在掌握其定义、性质的基础上，还需要通过大量的练习和实践来巩固所学知识。比如，可以尝试自己证明平行四边形的性质、解决与平行四边形相关的实际问题等。这些练习不仅有助于加深对平行四边形知识的理解，还能提高数学思维和解决问题的能力。

值得注意的是，平行四边形的定义和性质并非孤立存在。它们与三角形、圆形等其他几何图形之间存在着千丝万缕的联系。在学习平行四边形的过程中，不妨将其与其他几何图形进行对比分析，寻找它们之间的异同点，从而更加全面地理解和掌握几何知识。

总的来说，平行四边形作为几何学中的基础图形之一，其定义简洁明了、性质丰富多样、应用广泛深入。它不仅是数学家研究的对象、艺术家创作的灵感源泉、建筑师设计的灵感所在，更是我们学习数学、探索几何之美的得力助手。让我们一起走进平行四边形的世界，感受几何之美、探索数学之魅吧！

在结束这篇文章之前，不妨让我们再次回顾一下平行四边形的定义：两组对边分别平行的四边形。这简单的定义背后，隐藏着无数数学奥秘和几何之美。让我们带着这份好奇与热爱，继续在数学的世界里遨游、探索吧！