揭秘三角形中位线的神奇性质：中位线定理深度解析

三角形中位线定理：几何世界中的奇妙桥梁

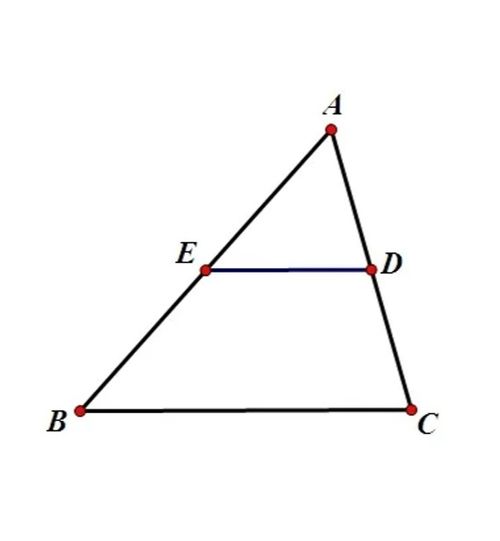
在几何学的广阔天地里，三角形作为最基础的图形之一，承载着无数令人着迷的定理和性质。其中，三角形中位线定理无疑是一颗璀璨的明珠，它以一种简洁而优雅的方式，揭示了三角形内部线段之间的奇妙关系。今天，就让我们一同走进三角形中位线定理的世界，探索它背后的奥秘和魅力。

一、初识中位线

首先，我们需要明确什么是三角形的中位线。在任意一个三角形中，连接任意两边中点的线段被称为该三角形的中位线。不妨设三角形为ABC，D、E分别为AB、AC的中点，那么线段DE就是三角形ABC的一条中位线。中位线的位置非常特殊，它总是平行于三角形的第三边，并且长度等于第三边的一半。

二、定理的陈述与证明

三角形中位线定理的完整表述是：三角形的中位线平行于第三边，并且等于第三边的一半。这个定理看起来简单，但背后却蕴含着深刻的几何意义。为了证明这个定理，我们可以采用多种方法，这里介绍一种常见的证明方式——向量法。

设三角形ABC的三个顶点坐标分别为A(x₁, y₁)、B(x₂, y₂)、C(x₃, y₃)，D、E分别为AB、AC的中点，则D的坐标为((x₁ + x₂)/2, (y₁ + y₂)/2)，E的坐标为((x₁ + x₃)/2, (y₁ + y₃)/2)。

根据向量的定义，我们可以得到向量AB = (x₂ - x₁, y₂ - y₁)，向量AC = (x₃ - x₁, y₃ - y₁)，向量DE = E - D = ((x₃ - x₁)/2 - (x₂ - x₁)/2, (y₃ - y₁)/2 - (y₂ - y₁)/2) = (x₃ - x₂)/2, (y₃ - y₂)/2)。

观察向量DE，我们发现它正好是向量BC = (x₃ - x₂, y₃ - y₂)的一半，即DE = (1/2)BC。由于向量DE与向量BC平行（方向相同或相反），因此我们可以得出中位线DE平行于第三边BC，并且长度等于BC的一半。

当然，除了向量法外，我们还可以利用平行四边形的性质、相似三角形的性质等多种方法来证明三角形中位线定理。这些证明方法虽然路径不同，但最终都指向了同一个结论，彰显了数学定理的严谨性和统一性。

三、定理的应用

三角形中位线定理在几何学中有着广泛的应用。它不仅可以用来求解三角形的边长、面积等问题，还可以作为证明其他几何定理的辅助工具。下面，我们就来看看几个具体的应用实例。

应用实例一：求解三角形边长

已知三角形ABC的两条边长AB和AC，以及它们的中点D和E，我们可以利用三角形中位线定理来求解第三边BC的长度。具体做法是：先求出中位线DE的长度（根据D、E的坐标或利用其他已知条件），然后由于DE = (1/2)BC，所以BC = 2DE。

应用实例二：证明平行四边形的性质

在平行四边形ABCD中，对角线AC、BD相交于点O。我们可以连接AB、BC的中点E、F，然后利用三角形中位线定理来证明OE = OF、AE = CF等平行四边形的性质。这是因为OE和OF分别是三角形ABC和三角形BCD的中位线，根据定理它们分别平行于AC和BD并且长度等于它们的一半。由于AC和BD是平行四边形的对角线且互相平分，所以OE = OF、AE = CF等结论自然成立。

应用实例三：求解三角形面积

在已知三角形ABC的底边BC和该边上的高h的情况下，我们可以利用三角形中位线定理来求解三角形的面积。具体做法是：先求出BC的中点D，然后利用定理求出中位线AD的长度（由于AD是BC的一半且垂直于BC，所以AD = h/2）。最后，根据三角形面积公式S = (1/2) × 底 × 高，我们可以得到S = (1/2) × BC × (h/2) = (1/4) × BC × h。虽然这个例子中并没有直接用到中位线来求解面积（因为已经给出了高h），但是中位线在求解过程中起到了辅助构造的作用，帮助我们理解了三角形内部的结构和关系。

四、定理的