直接解答：点到直线的距离计算公式

在我们日常学习、工作甚至探索世界的旅程中，数学无疑是一座不可或缺的桥梁，它帮助我们以精准的语言描述自然界和人为创造的各种现象。而在几何学的广阔天地里，点、线、面等基本元素构建起了一座座精妙绝伦的知识宫殿。今天，我们就来轻松而深入地聊一聊其中一个既基础又重要的概念——“点到直线距离公式”，揭开它神秘而又实用的面纱。

初识距离之美

想象一下，你站在一个开阔的田野上，眼前有一条蜿蜒的小路（我们姑且称之为“直线”），而你站的位置就是一个点。此刻，你可能好奇，自己离这条小路到底有多远呢？这就是“点到直线距离”所要解决的问题。简而言之，它是用来计算平面内一个固定点到某条直线距离的精确数值的工具。

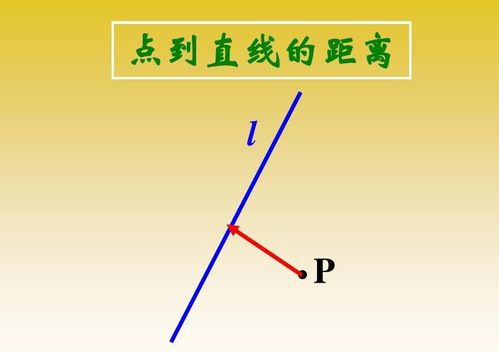
公式背后的智慧

点到直线距离公式的诞生，凝聚了数学家们的智慧与努力。它不仅仅是一个简单的数学表达式，更是几何学中向量、坐标系等多个知识领域交汇融合的结晶。具体来说，如果你熟悉坐标系（尤其是直角坐标系），那么这个问题就变得相对直观了。

在二维平面直角坐标系中，设直线方程为 `Ax + By + C = 0`（这是直线的一般式，其中A、B不同时为0），而点的坐标为 `(x0, y0)`。那么，点到这条直线的距离d，可以用以下公式计算：

\[

d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}

\]

这个公式看似复杂，但其实结构清晰，每部分都有其特定的意义。

`Ax0 + By0 + C` 部分：这其实是将点的坐标代入直线方程后的结果，它表示点到直线的“偏移量”。但注意，这里的偏移量可能是正也可能是负，取决于点在直线哪一侧，而我们需要的是绝对值距离，所以取其绝对值。

`\(\sqrt{A^2 + B^2}\)` 部分：这个根号下的表达式是直线法向量（即垂直于直线的向量）的模长。在几何意义上，它代表了直线方向的“伸缩因子”，确保距离计算的准确性。

如何使用这个公式

了解了公式的来龙去脉后，接下来就是如何应用它了。下面，我们通过一个简单的例子来演示：

假设有一条直线方程为 `3x - 4y + 12 = 0`，要求点 `(2, 3)` 到这条直线的距离。

1. 确定参数：直线方程为 `3x - 4y + 12 = 0`，点的坐标为 `(2, 3)`。

2. 代入公式：将A=3, B=-4, C=12, x0=2, y0=3代入点到直线距离公式。

3. 计算偏移量：首先计算 `3*2 - 4*3 + 12 = 6 - 12 + 12 = 6`。

4. 求模长：接着计算 `\(\sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)`。

5. 求距离：最后，距离d = `\(\frac{|6|}{5} = \frac{6}{5}\)`。

所以，点 `(2, 3)` 到直线 `3x - 4y + 12 = 0` 的距离是 `\(\frac{6}{5}\)` 单位长度。

公式的妙用与延伸

点到直线距离公式不仅仅是一个理论上的存在，它在许多实际应用场景中都有着举足轻重的地位。比如，在地理信息系统（GIS）中，经常需要计算某一地点到特定路径（可视为直线或折线）的最短距离；在建筑设计领域，评估某个固定点与建筑设计边界的距离，以确保安全距离；甚至在游戏开发中，计算角色与障碍物之间的距离，以实现碰撞检测等。

此外，这个公式还可以进一步延伸到其他领域，如向量分析、空间几何等，成为解决更复杂问题的基础工具。通过深入理解和灵活运用这个公式，我们可以更好地驾驭数学这把钥匙，打开通往更广阔知识世界的大门。

结语

总之，点到直线距离公式是几何学中一个简单却强大的工具，它连接了平面上的点与线，为我们提供了一种精确测量它们之间距离的方法。无论是在学术研究、工程技术还是日常生活中，它都展现出了广泛的应用价值和无限魅力。希望通过今天的分享，大家能够对这一公式有更深刻的认识和理解，并能在未来的学习和探索中灵活运用它，解锁更多未知的奥秘。