请问，惯性矩的计算公式具体是什么？

惯性矩计算公式详解

在物理学和工程学中，惯性矩（Moment of Inertia，简称I）是一个至关重要的概念，它描述了物体在旋转时抵抗改变其转动状态的性质。简单来说，惯性矩越大，物体在旋转时就越难改变其转速或方向。本文将详细探讨惯性矩的计算公式，并通过不同形状物体的实例，帮助读者全面理解这一概念。

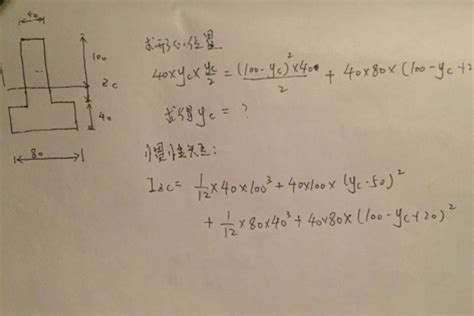
一、惯性矩的基本概念

惯性矩是物体相对于某一旋转轴的质量分布的量度，它取决于物体的质量和质心到旋转轴的距离。在数学上，对于点质量m，其惯性矩I可以表示为质量与质心到旋转轴距离r的平方的乘积，即I = m r^2。对于由多个点质量组成的复杂物体，其惯性矩则是所有点质量惯性矩的累加，即I = ∑mi ri^2。

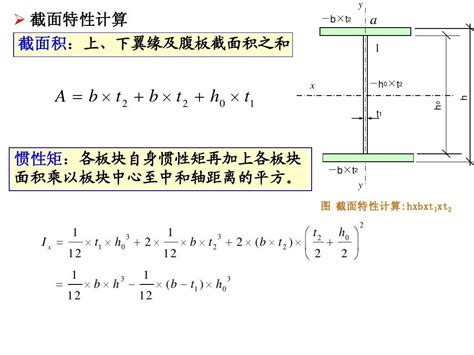
二、不同形状物体的惯性矩计算公式

1. 矩形

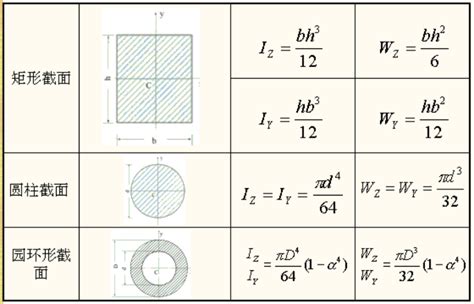
对于矩形截面，其惯性矩的计算公式取决于旋转轴的位置。若旋转轴通过矩形的中心且与长边平行，则惯性矩I可以表示为I = b*h^3/12，其中b为矩形的宽，h为高。若旋转轴沿矩形的边缘（例如沿长边），则惯性矩会有所不同，计算公式将变为I = 1/3 m a^2，其中a为矩形的边长（此处假设为长边），m为矩形的质量。

2. 三角形

对于等边三角形截面，若旋转轴垂直于三角形底边且通过其重心，其惯性矩I可以表示为I = b*h^3/36，其中b为底边长度，h为高。需要注意的是，这个公式假设了三角形是均匀的，即质量均匀分布在整个截面上。

3. 圆形

对于圆形截面，若旋转轴通过圆心且垂直于圆面，其惯性矩I可以表示为I = π*d^4/64，其中d为圆的直径。这个公式是基于圆截面质量的均匀分布推导出来的，适用于大多数圆形截面的情况。

4. 环形

对于环形截面（如空心圆柱的横截面），其惯性矩的计算稍微复杂一些。若旋转轴通过环心且垂直于环面，其惯性矩I可以表示为I = π*D^4*(1-α^4)/64，其中D为外圆的直径，d为内圆的直径，α = d/D。这个公式考虑了环形截面的内外径差异，能够准确反映环形截面在旋转时的惯性特性。

5. 其他形状

除了上述常见的形状外，还有其他一些复杂形状的惯性矩计算公式。例如，细长杆的惯性矩与其长度和质量的分布有关；圆柱体（无论是实心还是空心）的惯性矩则与半径和高度（或长度）有关。这些公式通常需要根据具体的形状和旋转轴位置进行推导。

三、惯性矩的应用

惯性矩在物理学和工程学中有广泛的应用。在机械设计中，了解物体的惯性矩有助于设计更加稳定和高效的旋转部件。例如，在设计汽车的发动机时，需要考虑曲轴和连杆的惯性矩，以确保它们在高速旋转时能够保持稳定并减少振动。

此外，在物理学中，惯性矩还与物体的旋转运动密切相关。根据角动量守恒定律，物体的角动量（即惯性矩与角速度的乘积）在不受外力矩作用时将保持不变。这一原理在滑冰、体操等运动项目中得到了生动的体现：滑冰运动员通过改变手臂的位置来改变自身的惯性矩，从而控制旋转速度；体操运动员在翻转时也需要精确控制身体的惯性矩以保持平衡和稳定。

四、结语

综上所述，惯性矩是描述物体旋转特性的重要参数之一。通过掌握不同形状物体的惯性矩计算公式，我们可以更加深入地理解物体的旋转运动规律及其在实际应用中的表现。无论是物理学研究还是工程设计领域都需要对惯性矩有深入的了解和掌握。希望本文能够帮助读者全面理解惯性矩计算公式及其应用。