如何计算相对原子质量

在微观世界的浩瀚星图中，原子，这一构成万物的基本单位，以其独特的魅力和复杂的性质吸引着无数科学家的探索与遐想。然而，当我们试图精确描述这些微小粒子的“重量”时，却遇到了一个难题：原子的实际质量太小了，小到几乎无法用我们日常所熟悉的单位来衡量。于是，一个更为巧妙且实用的概念应运而生——相对原子质量。那么，如何求解这个既神秘又实用的数值呢？让我们一起揭开它的面纱。

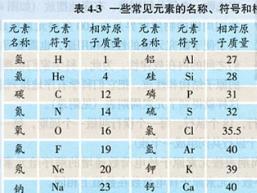
相对原子质量：微观世界的“重量秤”

想象一下，你手中握有一颗尘埃，而这颗尘埃里又包含了成千上万个原子。如果我们要直接测量这些原子的质量，那将是何等的艰巨任务！幸运的是，科学家们找到了一个巧妙的办法，即利用“相对原子质量”这一工具来间接表达原子的质量。

相对原子质量（Relative Atomic Mass，简称Ar），顾名思义，是一个相对值，它并不直接表示原子的实际质量，而是以一个特定原子——碳-12（即原子核中含有6个质子和6个中子的碳原子）的质量的1/12作为基准，来比较和衡量其他原子的质量。这个基准点如同微观世界中的“千克原器”，让我们能够以一种统一且易于理解的方式去描述和比较不同原子的“轻重”。

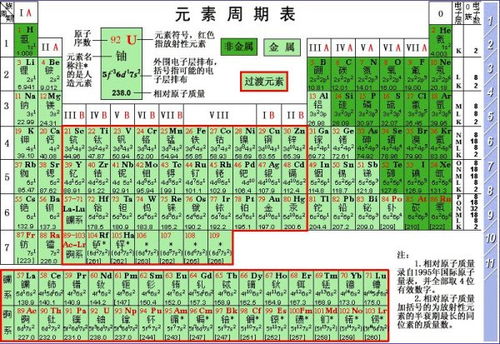
如何求解相对原子质量？

第一步：了解基准点

首先，我们要明确那个至关重要的基准点——碳-12原子的质量。科学家们已经精确测量出，一个碳-12原子的质量约为1.993×10⁻²⁶千克。而相对原子质量正是基于这个质量的1/12来定义的，即约为1.661×10⁻²⁷千克（也称为一个原子质量单位，符号为u或amu）。

第二步：寻找目标原子的实际质量

接下来，我们需要知道我们想要了解的那个原子的实际质量。这听起来似乎很难，但实际上，随着现代科技的发展，科学家们已经能够通过各种高精度仪器（如质谱仪）来测量出各种原子的精确质量。例如，氧原子的实际质量约为2.657×10⁻²⁶千克。

第三步：应用公式计算

有了基准点和目标原子的实际质量，我们就可以通过简单的比例关系来求解目标原子的相对原子质量了。公式如下：

\[ \text{相对原子质量} = \frac{\text{目标原子的实际质量}}{\text{碳-12原子质量的1/12}} \]

以氧原子为例，其相对原子质量的计算过程为：

\[ \text{氧的相对原子质量} = \frac{2.657×10⁻²⁶ \text{千克}}{1.661×10⁻²⁷ \text{千克}} \approx 16 \]

这样，我们就得到了氧原子的相对原子质量约为16。这个数值虽然是一个近似值，但已经足够我们在大多数情况下使用了。

相对原子质量的近似计算方法

除了上述的精确计算方法外，科学家们还发现了一个非常实用的近似公式，即：

\[ \text{相对原子质量} \approx \text{质子数} + \text{中子数} \]

这个公式虽然简单，但背后的原理却相当深刻。它基于原子核的组成（质子和中子）来估算原子的相对质量。因为质子和中子的质量都接近于原子质量单位，所以它们的数量之和可以作为原子相对质量的一个良好近似。当然，这个公式并不适用于所有情况，特别是对于那些拥有复杂同位素分布或电子排布异常的元素来说，但它在大多数情况下都是相当准确的。

相对原子质量的意义与应用

相对原子质量不仅是化学领域中的一个基本概念，也是连接宏观世界与微观世界的重要桥梁。它使得我们能够以一种统一且易于理解的方式去描述和比较不同原子的性质和行为。在化学计算、物质分析、药物研发等众多领域中，相对原子质量都发挥着不可或缺的作用。

例如，在化学反应中，相对原子质量可以帮助我们计算反应物和生成物的质量比；在药物研发中，了解药物的相对分子质量则有助于我们评估其药效和安全性。可以说，相对原子质量是科学家们探索微观世界、揭示物质本质的重要工具之一。

结语

通过上述的介绍，我们不难发现，相对原子质量虽然是一个看似抽象且复杂的概念，但实际上却蕴含着深刻的物理意义和广泛的应用价值。它不仅是化学领域中的一个核心概念，也是连接宏观世界与微观世界的重要纽带。希望本文能够激发你对微观世界的兴趣，让你在探索未知的路上迈出更坚实的一步。