如何计算球体的体积?
在探讨“球体的体积是什么”这一数学与几何学的核心概念时,我们首先需要从基础定义出发,逐步深入,让即便是非数学专业的读者也能轻松理解其精髓。球体,作为三维空间中一种完美对称的几何体,不仅在生活中随处可见(如篮球、足球、地球等),更是许多科学计算和工程设计中的重要元素。接下来,让我们一同揭开球体体积的神秘面纱。

一、球体的基本定义
球体,简单来说,是一个由所有距离一个固定点(称为球心)相等的点组成的立体图形。这个固定的距离被称为球的半径,记作r。球体没有平面边界,而是完全由曲面构成,这种曲面被称为球面。球面上的每一点到球心的距离都等于r,这赋予了球体独特的完美对称性和连续性。

二、球体体积的探索历程
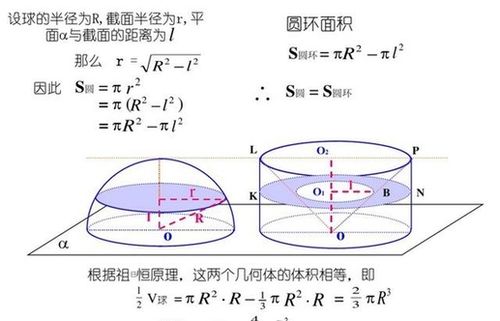
历史上,对于球体体积的精确计算并非一蹴而就。古希腊数学家阿基米德(Archimedes)是首位系统研究并准确推导出球体体积公式的人。他通过巧妙地将球体与圆柱体(底面半径和高都与球体半径相等)和圆锥体(底面半径和高也与球体半径相等)的关系相结合,利用排水法原理,得出了球体体积等于其外接圆柱体体积的三分之二,同时也等于其内切圆锥体体积的四倍的结论。这一发现,不仅展示了数学推理的力量,也深刻影响了后续几何学的发展。
三、球体体积的计算公式
基于阿基米德的研究成果,我们可以得出球体体积的计算公式为:
\[ V = \frac{4}{3}\pi r^3 \]
其中,V代表球体的体积,r是球体的半径,π(Pi)是一个无理数,约等于3.14159...,它表示圆的周长与直径之比。这个公式简洁而优雅,是数学中几何体积计算的基石之一。
四、理解球体体积公式的意义
半径的影响:从公式中可以看出,球体体积与半径的三次方成正比。这意味着,当球体的半径增加时,其体积的增长速度远快于表面积的增长。例如,如果球体的半径加倍,其体积将变为原来的8倍(因为\(2^3=8\)),而表面积仅变为原来的4倍(圆的面积公式为\(\pi r^2\))。
π的角色:π作为圆周率的简称,在球体体积公式中扮演了关键角色。它反映了圆及与之相关的三维形状(如球体)的固有性质,是连接二维与三维几何的桥梁。
对称性与完美性:球体体积的计算公式体现了球体作为三维空间中最完美对称形状的特质。无论从哪个方向观察或测量,其体积都是恒定的,这种特性在物理、工程和天文学等领域有着广泛的应用。
五、球体体积的实际应用
物理学:在计算物质占据的空间大小时,特别是当物质形状接近球体时(如行星、恒星、雨滴等),球体体积公式成为不可或缺的工具。
工程学:在建筑设计、机械制造、航空航天等领域,需要精确计算球形部件或结构的体积,以确保设计的合理性和材料使用的经济性。
医学:在医学影像学中,通过分析CT或MRI扫描得到的球形病变区域,医生可以利用球体体积公式估算其大小,辅助诊断和治疗。
日常生活:从计算足球场的草坪用量到估算水缸中水的体积,球体体积的概念虽不直接显现,但其背后的原理却无处不在。
六、结语
通过上述的探讨,我们不难发现,“球体的体积是什么”这一问题,不仅关乎数学公式的推导与运用,更蕴含着深刻的几何美学、物理原理以及广泛的应用价值。球体作为自然界与人类文明中不可或缺的一部分,其体积的计算不仅是数学教育的重要内容,也是连接理论与实践、抽象与具象的桥梁。希望这篇文章能帮助您更全面地理解球体体积的奥秘,激发您对几何学和数学世界的进一步探索兴趣。
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/03
-
03/03
-
03/03
-
03/03
-
03/03









