揭秘！如何轻松判断两个数是否互质？

在数学的广阔天地里，互质数是一个既基础又重要的概念，它关乎于两个数之间最纯粹的数学关系——除了1以外没有其他公因数。掌握如何判断两个数是否互质，不仅能帮助我们更好地理解数的性质，还能在解决数学问题、编程、密码学等多个领域发挥关键作用。本文将从定义出发，结合理论分析与实例演示，多维度地探讨如何判断两个数是否互质。

一、互质数的定义与基础理解

首先，我们需要明确互质数的定义：如果两个正整数a和b的最大公因数（GCD, Greatest Common Divisor）为1，则称a和b是互质的，或称a与b互质。这个概念的核心在于“除了1以外没有其他公因数”，这意味着两个数在数的分解上具有高度的独立性。

二、直观判断法：小数字直接观察

对于较小的数字，我们可以通过直接观察法来判断它们是否互质。例如，判断6和7是否互质，我们可以列出它们各自的因数：6的因数有1、2、3、6，而7的因数只有1和7。显然，除了1以外，它们没有其他共同的因数，因此6和7是互质的。这种方法简单直接，适用于小数字的快速判断。

三、因数分解法：深入本质

对于较大的数字，直接观察法可能不再适用，此时我们可以采用因数分解法。因数分解是将一个数分解为几个质数的乘积的过程。如果两个数的质因数集合没有交集（除了1这个共同因数），则这两个数互质。例如，判断24（=2×2×2×3）和35（=5×7）是否互质，我们发现24的质因数有2和3，而35的质因数有5和7，它们的质因数集合没有交集，所以24和35是互质的。

四、辗转相除法（欧几里得算法）：高效计算

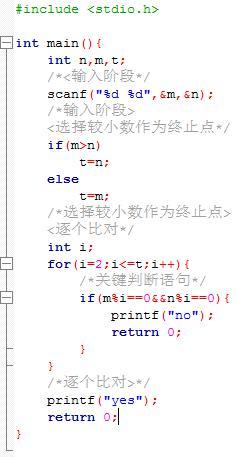
在实际应用中，我们更常用到的是辗转相除法（也称欧几里得算法）来判断两个数是否互质。该算法基于一个重要定理：两个正整数的最大公因数等于其中较小数和两数相除余数的最大公因数。具体步骤如下：

1. 初始化：设两个数为a和b（假设a>b）。

2. 取余：计算a除以b的余数，记为r。

3. 判断：如果r=0，则b即为a和b的最大公因数；否则，将b的值赋给a，r的值赋给b，重复步骤2。

4. 结论：当最终余数为0时，得到的最大公因数若为1，则a和b互质。

例如，判断128和75是否互质：

128÷75=1...53（余数53）

75÷53=1...22（余数22）

53÷22=2...9（余数9）

22÷9=2...4（余数4）

9÷4=2...1（余数1）

4÷1=4...0（余数0，此时a=4, b=1）

由于最终余数为0，且此时的最大公因数为1，所以128和75是互质的。

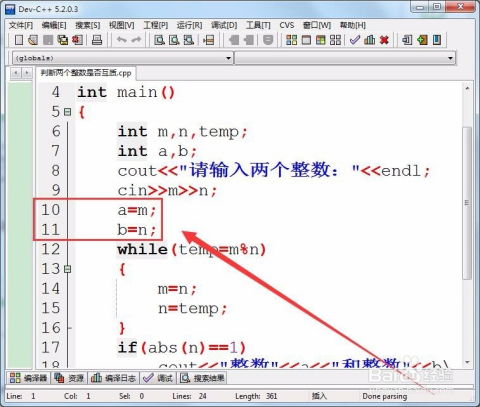
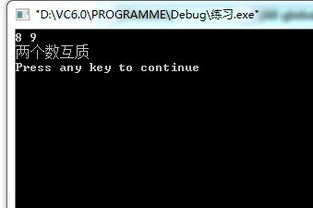
五、编程实现：自动化判断

在计算机科学领域，判断两个数是否互质的问题可以通过编写程序自动化解决。利用上述的辗转相除法，我们可以轻松编写出相应的代码。以下是一个简单的Python示例：

```python

def gcd(a, b):

while b != 0:

a, b = b, a % b

return a

def are_coprime(a, b):

return gcd(a, b) == 1

测试

print(are_coprime(128, 75)) 输出: True

```

这段代码首先定义了一个`gcd`函数来计算两个数的最大公因数，然后定义了一个`are_coprime`函数来判断这两个数是否互质。通过调用`are_coprime`函数并传入待判断的两个数，程序将输出它们是否互质的结果。

六、应用实例：拓展思维

互质数的概念不仅在纯数学理论中占据重要地位，还在多个实际应用场景中发挥作用。例如，在密码学中，选取两个大的互质数作为密钥的一部分，可以极大地增加密码的安全性，因为即使知道其中一个数，要找到与之互质的另一个大数也并非易事。此外，在组合数学、数论研究等领域，互质数的性质也经常被