揭秘！正三棱锥究竟是什么神秘几何体？

正三棱锥，这一几何形体，在三维空间中以其独特的形态和性质吸引着无数数学爱好者的目光。它不仅是几何学研究中的一个基本模型，也是理解更复杂三维图形结构的重要基石。下面，我们就来深入探讨一下“什么是正三棱锥”，以及它的一些基本特性和应用场景。

定义探索

正三棱锥，顾名思义，是由一个正三角形作为底面，并与底面不共线的三个顶点通过线段（即棱）相连而成的三维多面体。这里的“正”字，强调了底面三角形的三边等长且三个内角均为60°，同时，从顶点垂直到底面的高（也称为棱锥的高）会将底面正三角形划分为三个全等的等腰三角形，且这三个等腰三角形的底边即为底面的三边，腰长则等于棱锥的侧棱长。

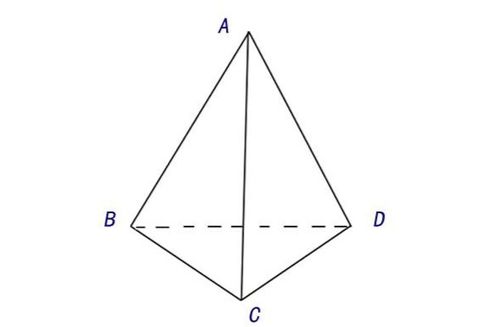
基本性质

1. 底面特性：正三棱锥的底面是一个正三角形，具有高度的对称性，其三条中线、三条高线、三条角平分线、三条垂直平分线以及三条对称轴均重合于一点，即三角形的重心、内心、外心、垂心及旁心，这一点也称为三角形的中心。

2. 侧棱等长：正三棱锥的四个面中，除了底面外，其余三个侧面均为全等的等腰三角形，这意味着从顶点出发的三条侧棱长度相等，进一步增强了整个形体的对称性。

3. 高与体积：棱锥的高是连接顶点与底面中心并垂直于底面的线段。利用这一高度，结合底面正三角形的面积，我们可以计算出正三棱锥的体积。具体地，体积V = (1/3) × 底面积 × 高，其中底面积可通过正三角形的边长使用海伦公式或直接公式计算得出。

4. 外接球与内切球：正三棱锥不仅具有唯一的外接球（即存在一个球，使得棱锥的所有顶点都在球面上），还存在内切球（即球与棱锥的五个面都相切）。这两个球的存在性及其性质的探讨，是几何学中的有趣话题。

5. 对称性：由于底面是正三角形且侧棱等长，正三棱锥展现出高度的旋转对称性和镜面对称性。围绕其高线旋转120°或240°，棱锥的形态保持不变；同时，通过底面三角形的三条对称轴进行镜面反射，也能得到与原棱锥重合或镜像对称的图形。

应用领域

正三棱锥不仅在纯粹的数学研究中占据一席之地，其独特的形态和性质也使其在多个领域得到应用：

建筑设计：在建筑设计中，正三棱锥或其变形体常被用作屋顶结构，如金字塔式的建筑设计，就巧妙地利用了正三棱锥的稳定性和视觉冲击力，赋予建筑以独特的艺术美感。

工程结构：在桥梁、塔架等工程结构中，正三棱锥或其衍生结构（如三棱台）因其良好的稳定性和承重能力而被广泛应用。通过合理设计，这些结构能够有效地分散载荷，提高整体结构的强度和稳定性。

艺术雕塑：雕塑艺术家们也经常利用正三棱锥的形态进行创作，通过抽象或具象的手法，将这一几何形体转化为富有感染力的艺术作品，传达出特定的情感和意境。

教育教具：在数学和物理教学中，正三棱锥作为教具，有助于学生直观理解三维空间中的点、线、面关系，以及几何体的性质、计算等问题，是培养学生空间想象力和逻辑思维能力的重要工具。

结语

综上所述，正三棱锥作为三维空间中的一个基本而又独特的几何形体，不仅具有丰富的数学性质，还在建筑设计、工程结构、艺术雕塑以及教育等多个领域展现出广泛的应用价值。通过对正三棱锥的深入了解和探索，我们不仅能够加深对三维空间几何学的认识，还能激发创新思维，将理论知识应用于实践之中，创造出更多具有实用价值和艺术美感的作品。