如何计算正三棱锥的高度?
在探索几何学的奇妙世界中,正三棱锥作为一个基础而富有魅力的立体图形,其形态之稳定、结构之和谐,总能激发人们无尽的遐想与探索欲。当我们聚焦于“正三棱锥的高是多少”这一问题时,实际上是在深入解析这一几何体的内在属性与外在特征,通过多维度的视角,揭开其高度的神秘面纱。
一、定义与基本性质
首先,让我们明确正三棱锥的定义:正三棱锥是指底面为正三角形,且顶点在底面的射影为底面正三角形中心的三棱锥。这一简洁而精确的定义,为我们后续探讨其高度奠定了基础。
正三棱锥具有几个显著的基本性质:其侧面为三个全等的等腰三角形,且这三条侧棱两两等长;底面为正三角形,具有高度的对称性;顶点到底面的距离,即我们通常所说的“高”,是连接顶点与底面正三角形中心的垂线段。
二、高度的几何计算
1. 直观构造法
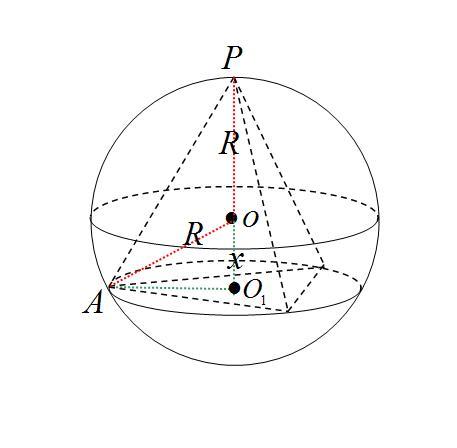
为了直观理解并计算正三棱锥的高,我们可以尝试构建一个辅助平面,该平面过顶点并垂直于底面。这一操作实际上是在三维空间中“切割”出一个二维截面,便于我们观察与测量。在截面图中,正三棱锥的高直接表现为从顶点垂直到底面中心的线段,与底面构成一个直角三角形。利用勾股定理,在已知底面边长或侧棱长等条件下,我们可以计算出这个高度。
2. 代数解析法
对于更复杂的情境,如侧棱长与底面边长关系不明确的正三棱锥,我们可以采用代数解析法。设底面边长为a,侧棱长为l,高为h。通过建立直角坐标系,利用向量或空间几何中的距离公式,可以建立关于h的方程。这些方程通常涉及到底面正三角形的性质(如边长、高、中心角等)以及侧棱与底面之间的关系。解这类方程,虽然过程可能稍显繁琐,但能准确求出h的值。
三、高度的物理意义与应用
1. 物理稳定性
正三棱锥的高度,从物理学的角度来看,直接关联到其整体的稳定性。较高的正三棱锥,在受到外力作用时,由于重心较高,可能更容易发生倾覆。反之,适当降低高度,可以增强其稳定性,这一原理在建筑设计、工程结构等领域有着广泛的应用。
2. 光学与声学应用
在某些特定领域,如光学或声学研究中,正三棱锥的形状及其高度可能作为设计元素之一,影响光线的反射、折射或声音的传播。例如,在舞台灯光设计中,利用正三棱锥形状的反射镜,可以创造出独特的光影效果;在声学设计中,调整正三棱锥结构的高度,可以改变声场的分布,优化音响效果。
四、数学与美学的融合
正三棱锥不仅是一个几何体,更是数学与美学完美结合的典范。其高度的计算,不仅仅是数值上的求解,更是对几何美、对称美的一种探索与体现。在数学课堂上,通过讨论正三棱锥的高度,可以引导学生感受几何图形的魅力,培养空间想象能力和逻辑思维能力。同时,在艺术创作中,正三棱锥的形态也常常作为灵感来源,被赋予丰富的文化内涵和象征意义。
五、结语
综上所述,“正三棱锥的高是多少”这一简单问题,实则蕴含着丰富的数学内涵与广泛的应用价值。从几何计算到物理意义,从数学美学到实际应用,正三棱锥的高度成为连接多个学科领域的桥梁。在探索与解答这一问题的过程中,我们不仅学会了如何运用数学知识解决实际问题,更深刻体会到了几何之美与数学之趣。正如每一个几何体都有其独特的魅力所在,正三棱锥的高度,正是这魅力中不可或缺的一部分。
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/04
-
03/04
-
03/04
-
03/04
-
03/04










