揭秘！你不可不知的素数真相：它究竟是什么？

在数学的浩瀚星空中，有一类数字如同夜空中最亮的星，它们简单、纯粹，又藏着无尽的奥秘，这就是——素数。想象一下，当你尝试将一个数字除以比它小的每一个正整数，却只能得到1和它本身作为商时，这个数字就仿佛在数学界里宣布了自己的“独一无二”，它，就是素数。

素数的定义：简单而深刻的起点

首先，让我们用最简单的方式来理解素数。素数，又称质数，是大于1的自然数中，除了1和它本身以外不再有其他因数的数。换句话说，一个数如果只能被1和它自己整除，那么这个数就是素数。比如2、3、5、7、11等，它们都是素数家族的成员。而像4、6、8、9这样的数，因为除了1和它们自身外，还能被其他数整除（比如4能被2整除，6能被2和3整除），所以它们不是素数，被称为合数。

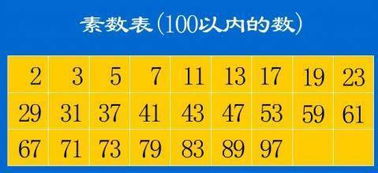
素数的魅力：数学的基础砖石

素数之所以引人入胜，不仅仅是因为它们的简单定义，更在于它们在数学大厦中扮演的基石角色。从古老的数学定理到现代密码学，素数的身影无处不在。比如，欧几里得的《几何原本》中就提到了关于素数的无限性证明，即存在无穷多个素数。这一结论看似简单，却是数学逻辑严密性的重要体现。

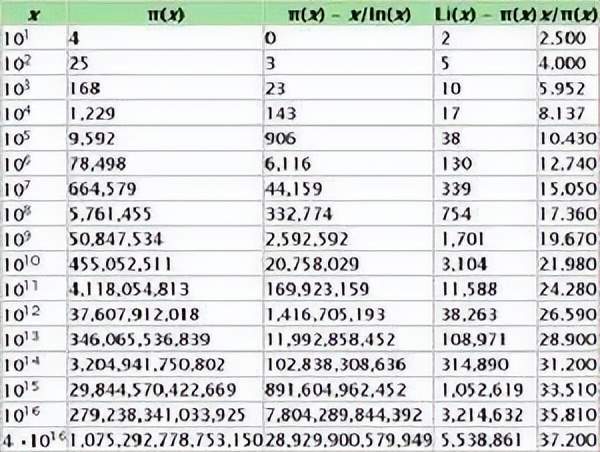
在更高级的数学领域，素数更是不可或缺。比如数论——数学中专门研究整数性质的分支，几乎每一个重大发现都离不开对素数的深入研究。素数分布定理、孪生素数猜想、哥德巴赫猜想等，这些听起来就充满神秘感的数学问题，无一不围绕着素数展开。

素数的实际应用：从理论到现实的桥梁

除了理论上的重要性，素数在现实世界中也有着广泛的应用。最引人注目的莫过于密码学领域。现代互联网安全的基础——公钥加密体系，就大量使用了素数。比如RSA加密算法，它依赖于寻找两个大的素数并计算它们的乘积来生成公钥和私钥。由于分解大素数乘积比找到两个这样的素数要困难得多，因此这种加密方式被认为是相对安全的。

此外，素数在编程和算法设计中也有着重要应用。比如，在排序算法中，有时利用素数的特性可以减少比较次数，提高算法效率。而在某些哈希函数的设计中，选择合适的素数作为模数，可以减少碰撞的发生，提高数据的检索速度。

寻找素数的艺术：从手算到计算机的飞跃

历史上，人们寻找素数的方法经历了从手算到计算机辅助的巨大飞跃。早期的数学家们通过试除法，一个个地检查每个数是否为素数。然而，随着数字的增长，这种方法变得越来越低效。到了现代，随着计算机技术的飞速发展，人们开发出了一系列高效的素数寻找算法，如埃拉托斯特尼筛法（Sieve of Eratosthenes）、轮询筛法（Wheel Sieve）以及更复杂的算法，如数域筛法（Number Field Sieve）等，这些算法极大地提高了寻找大素数的速度和效率。

素数的未来：未解之谜与无限可能

尽管我们已经对素数有了相当深入的了解，但素数领域仍有许多未解之谜等待着我们去探索。比如，孪生素数猜想——是否存在无穷多对相差为2的素数对？再比如，素数在自然数中的分布规律是怎样的？这些问题看似简单，实则深奥无比，它们激发了无数数学家的好奇心和求知欲。

同时，随着科技的发展，素数的研究也在不断拓展新的应用领域。比如，在量子计算领域，素数的研究有望为开发更加安全的加密算法提供新的思路。而在人工智能和大数据等新兴技术的推动下，素数也可能在更多领域展现出其独特的价值。

结语

素数，这个简单而又复杂的数学概念，不仅是我们理解数学世界的一把钥匙，更是连接理论与实践、过去与未来的桥梁。从古老的数学定理到现代科技的广泛应用，素数始终以其独特的魅力吸引着无数人的目光。让我们一同走进素数的世界，感受那份纯粹与深邃吧！