如何计算圆柱体的体积?
当我们谈及圆柱体的体积计算时,这是一个既基础又实用的数学问题,广泛应用于建筑、工程、物理学及日常生活中的多个领域。无论是设计一个储水塔,还是计算一个管道内流体的容量,掌握圆柱体体积的计算方法都显得尤为重要。下面,我们就直接切入主题,以简洁明了的方式介绍如何计算圆柱体的体积。
圆柱体体积的基本公式
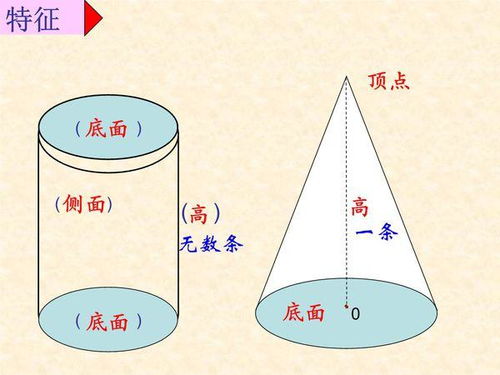
圆柱体,顾名思义,是一个由两个平行且等大的圆形底面以及连接这两个底面的侧面围成的立体图形。要计算其体积,我们需要知道两个关键参数:底面的半径(r)和高(h)。
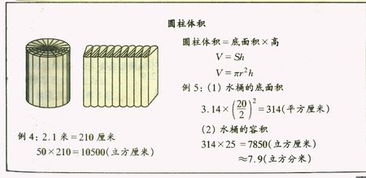
圆柱体体积的计算公式是:
$$V = \pi \times r^2 \times h$$
其中,$V$ 代表体积,$\pi$(Pi)是一个特殊的数,约等于3.14159...,代表圆周长与直径之比,而 $r$ 是底面圆的半径,$h$ 是圆柱体的高。
逐步理解公式
1. $\pi$ 的作用:在圆柱体体积的计算中,$\pi$ 用于将底面圆的面积($\pi r^2$)转换为具体的数值。圆的面积是所有扇形面积之和,而扇形的面积又与圆心角和半径有关,最终可推导出圆的面积公式为 $\pi r^2$。
2. 底面面积的计算:首先,我们需要知道圆柱体底面的面积。由于底面是一个圆,所以其面积 $A = \pi r^2$。这里的 $r$ 是底面圆的半径,即从圆心到圆上任意一点的距离。
3. 高度的影响:圆柱体的体积是其底面面积沿着高度方向的累积。想象一下,如果你有一个很薄的圆片,随着圆片数量的增加(且每个圆片之间的距离逐渐减小),最终堆叠起来就形成了一个圆柱体。这些圆片的总面积(即所有圆片面积之和)就是圆柱体的体积。因此,将底面面积乘以高度 $h$,就得到了圆柱体的体积。
应用实例
假设我们有一个半径为5厘米,高为10厘米的圆柱体,我们需要计算它的体积。
1. 确定参数:$r = 5$ 厘米,$h = 10$ 厘米,$\pi$ 取3.14(为简化计算)。
2. 计算底面面积:$A = \pi r^2 = 3.14 \times 5^2 = 3.14 \times 25 = 78.5$ 平方厘米。
3. 计算体积:$V = A \times h = 78.5 \times 10 = 785$ 立方厘米。
因此,这个圆柱体的体积是785立方厘米。
注意事项
单位的一致性:在计算过程中,确保所有参数(如半径、高度)的单位相同,否则需要先统一单位再进行计算。
$\pi$ 的取值:在实际应用中,$\pi$ 的取值可以根据需要精确到不同的小数位数。在大多数情况下,取到小数点后几位(如3.14或3.14159)已经足够精确。
实际应用:圆柱体体积的计算不仅限于理论学习,更广泛应用于各种实际问题中。比如,在建筑设计中估算材料用量,或在物理学中分析流体的存储和流动情况等。
通过上述介绍,相信您已经掌握了圆柱体体积的计算方法。无论是在学习、工作还是日常生活中,这个简单而强大的公式都能为您提供帮助。
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/07
-
02/07
-
02/07
-
02/07
-
02/07









