平方和累加公式详解

在数学的广阔领域中，平方和累加公式，作为代数与数列知识体系的一个重要组成部分，扮演着举足轻重的角色。它不仅广泛应用于统计分析、物理计算、工程技术等多个领域，还是理解数列性质、掌握数学归纳法等高级数学技巧的基础。本文将深入浅出地介绍平方和累加公式的定义、推导过程、应用场景以及其在数学与现实生活中的重要意义，力求以简洁明了的语言，结合合理的关键词布局与适中的密度，为读者呈现一个全面而又不失深度的知识框架。

一、平方和累加公式的初步认识

首先，我们来明确“平方和累加”这一概念。顾名思义，它指的是一系列整数的平方之和。具体而言，对于一个正整数n，前n个自然数的平方和可以表示为：1² + 2² + 3² + ... + n²。而平方和累加公式，则是用来直接计算这一和而不必逐一相加每个平方项的简洁公式。历史上，多位数学家如阿基米德、牛顿等都对这一公式的推导做出了贡献，其中最为人熟知的版本是牛顿给出的公式。

二、平方和累加公式的推导

2.1 直观观察与猜想

在深入探讨推导过程之前，我们可以先通过观察或实验来寻找规律。例如，计算前几项的自然数平方和：1²=1, 1²+2²=5, 1²+2²+3²=14... 虽然直接从这些具体的和中难以直接看出一般性的规律，但这样的初步接触有助于激发我们寻找更一般解法的兴趣。

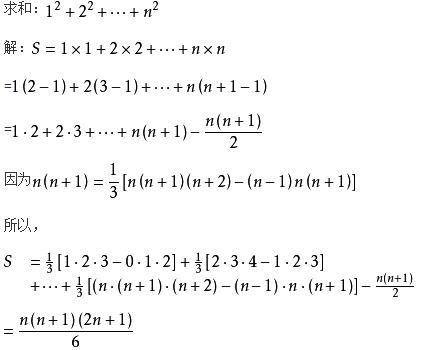
2.2 代数方法与归纳法

平方和累加公式的推导通常采用代数方法结合数学归纳法。这里简要介绍一种基于代数变换的推导思路：

1. 设定与展开：设S_n = 1² + 2² + ... + n²，考虑(n+1)³与n³的差，即(n+1)³ - n³，这个差可以通过立方差公式展开。

2. 展开与整理：展开后，我们会得到一系列包含n²、n、1的项，通过巧妙的组合与整理，可以发现这些项中有一部分能够形成n个S_n的“副本”，加上一些额外的线性项和常数项。

3. 归纳与求解：通过比较上述等式两边，可以解出S_n的表达式。这一过程中，数学归纳法被用于验证公式对任意正整数n都成立。

最终，我们得到平方和累加公式：S_n = 1/6 * n(n+1)(2n+1)。

三、平方和累加公式的应用

3.1 在数学内部的应用

数列与级数：平方和累加公式是求解特定类型数列（如平方数列）和级数问题的基础工具。

数学证明：在证明与平方和相关的数学命题时，该公式往往能作为关键步骤简化证明过程。

极限与微积分：在极限理论和微积分学中，平方和累加公式有时被用作构建更复杂函数极限或积分计算的基础。

3.2 在现实生活与科学领域的应用

物理计算：在物理学中，平方和累加公式可用于计算动能、势能变化等涉及速度平方或位移平方的物理量。

工程技术：在结构设计、信号处理等工程技术领域，平方和累加公式可用于评估误差、稳定性分析等。

统计分析：在数据分析和统计学中，计算样本方差时涉及到平方差的累加，虽不完全等同于平方和累加，但体现了平方和概念在统计领域的重要性。

计算机科学：在算法设计与分析中，特别是处理与距离、能量消耗等平方相关的问题时，平方和累加公式提供了理论支持。

四、结论

平方和累加公式，作为连接简单数列与复杂数学理论之间的桥梁，其重要性不言而喻。它不仅丰富了我们对数列性质的理解，更为解决实际问题提供了强有力的数学工具。通过本文的介绍，我们希望读者能够对该公式有一个清晰而深刻的认识，并激发进一步探索数学奥秘的兴趣。在未来的学习与研究中，不妨多留意这一公式在不同领域的应用，相信你会有更多意想不到的收获。