揭秘！平方和累加公式的魔力：让数字运算变简单的秘密武器

在数学的奇妙世界里，隐藏着许多有趣而实用的公式，它们如同通往智慧之门的钥匙，帮助我们解决复杂问题，简化计算过程。今天，我们就来聊聊一个既常见又重要的概念——“平方和累加公式”，用通俗易懂的语言，一步步揭开它的神秘面纱。

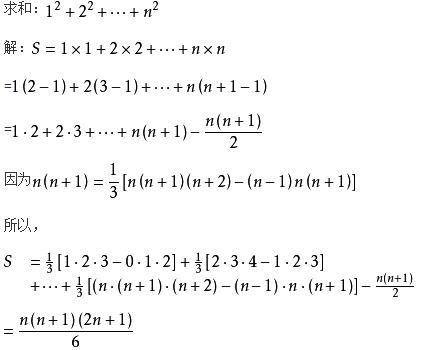
一、初探平方和

首先，我们得从“平方”这个概念说起。平方，简单来说，就是一个数乘以它自己。比如，4的平方就是4乘以4，等于16。在日常生活中，平方可能不那么直观，但在数学、物理乃至经济学等多个领域，它都扮演着举足轻重的角色。

那么，“平方和”又是什么呢？顾名思义，就是几个数的平方加在一起的结果。比如，1的平方是1，2的平方是4，那么1和2的平方和就是1+4=5。这个概念看似简单，但当我们需要计算一系列数的平方和时，手动计算就会变得繁琐且容易出错。这时候，平方和累加公式就显得尤为重要了。

二、平方和累加公式的登场

平方和累加公式，也被称为平方数列求和公式，是一个能够直接计算出从1到n的所有整数的平方和的数学表达式。这个公式不仅简化了计算过程，还揭示了平方数列求和背后的深层规律。

具体来说，从1加到n的平方和可以用以下公式表示：

$$1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}$$

这个公式看起来有些复杂，但别急，我们一步步来解读它。

三、公式的推导（非专业深度，适合大众理解）

虽然平方和累加公式的推导涉及较为复杂的数学方法（如数学归纳法、代数变换等），但我们可以通过一个相对直观的方式来理解其背后的逻辑。

想象一下，你有一个正方形的网格，每个小格代表一个数的平方。当你从1开始，逐渐增加数字并计算其平方，然后将这些平方值作为网格中相应位置的小方块大小（或面积），你会发现这些“方块”的排列和累加呈现出某种规律性。

数学家们通过深入研究这些规律，结合代数技巧，最终得出了上述公式。虽然这个推导过程对于非数学专业的朋友来说可能稍显晦涩，但我们可以确信的是，这个公式是正确的，并且非常有用。

四、公式的应用

平方和累加公式在实际应用中有着广泛的用途。以下是几个典型的例子：

1. 物理学：在计算物理问题时，如动能、势能等与距离平方相关的能量变化，平方和累加公式能够帮助我们快速得出结果。

2. 统计学：在数据分析中，当需要计算样本数据的平方和时，该公式可以大大提高计算效率，特别是在处理大量数据时。

3. 计算机科学：在算法设计中，尤其是在涉及优化、排序等问题时，平方和累加公式有时可以作为评估算法性能的一个指标。

4. 日常生活：虽然日常生活中不常直接用到这个公式，但了解它背后的数学原理可以培养我们的逻辑思维能力，让我们在面对复杂问题时更加从容不迫。

五、如何记住这个公式？

对于许多人来说，记忆复杂的数学公式可能是一个挑战。不过，我们可以通过一些方法来帮助记忆平方和累加公式：

联想记忆：将公式中的各项与生活中的事物相联系，比如“n(n+1)(2n+1)”可以想象成三个连续年份的乘积（当然，这只是一个形象化的比喻，并非实际含义）。

重复练习：通过反复练习使用公式解决问题，加深对公式的理解和记忆。

理解原理：虽然公式的推导过程可能复杂，但理解其背后的数学原理是长久记忆的关键。尝试从多个角度去理解这个公式，比如通过图形直观感受平方和的变化规律。

六、结语

平方和累加公式，这个看似简单的数学表达式，背后蕴含着丰富的数学知识和深刻的规律。它不仅是数学研究的一个重要工具，也是连接数学与现实生活的桥梁。希望通过今天的介绍，大家能够对平方和累加公式有一个更加清晰、深入的认识，并在未来的学习和生活中灵活运用它。

记住，数学不仅仅是数字和公式的堆砌，更是思维的体操和智慧的火花。让我们一起在数学的海洋中遨游，探索更多未知的奥秘吧！