数列求和的高效方法与经典公式详解
在探讨数列求和的众多方法中,掌握几种基础且高效的方法对于解决各类数学问题至关重要。本文将详细介绍数列求和的七种主要方法及相关公式,旨在帮助读者深入理解并灵活应用这些技巧,提高解题能力和阅读体验。同时,注重内容结构的逻辑性和关键词的合理分布,以增强文章的可读性和搜索引擎友好度。
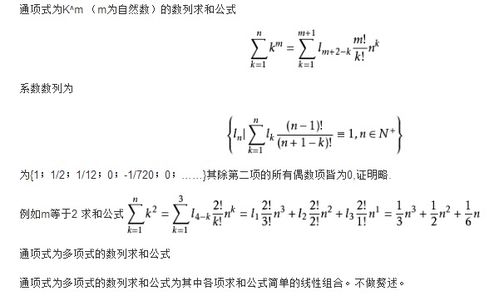
一、公式法
公式法是最基础也是最常用的数列求和方法,特别适用于等差数列和等比数列。
等差数列求和公式:设等差数列的首项为$a_1$,公差为$d$,项数为$n$,则前$n$项和$S_n$的公式为:
$$ S_n = \frac{n}{2}(2a_1 + (n-1)d) = \frac{n(a_1 + a_n)}{2} $$
其中,$a_n$是数列的第$n$项,等于$a_1 + (n-1)d$。
等比数列求和公式:设等比数列的首项为$a_1$,公比为$q$,项数为$n$(注意$q \neq 1$),则前$n$项和$S_n$的公式为:
$$ S_n = \frac{a_1(1 - q^n)}{1 - q} $$
当$q = 1$时,$S_n = na_1$。
二、分组求和法
分组求和法适用于数列的各项之间存在一定规律,可以将数列拆分成若干个等差、等比或其他易于求和的子数列,再分别求和后相加。例如,数列1, 3, 2, 7, 4, 11, ... 可以分成奇数项和偶数项两个等差数列进行求和。
三、倒序相加法
倒序相加法适用于首尾两端等“距离”的两项和相等或等于同一常数的数列。通过将数列倒序排列后与原数列相加,利用对称性简化求和过程。等差数列求和公式的推导就采用了此方法。
四、错位相减法
错位相减法主要用于求解形如$A_n = B_nC_n$的数列和,其中${B_n}$是等差数列,${C_n}$是等比数列。通过对数列${A_n}$求和,列出和式$S_n$,再将其各项同乘等比数列的公比$q$,错位相减后得到数列的和。
五、裂项相消法
裂项相消法通过将数列的通项拆分成两项之差,在求和过程中使中间项相互抵消,从而简化计算。这种方法特别适用于分式形式的数列,如$\frac{c}{an(an+1)}$(其中$c$为常数),可以通过裂项化为两项之差进行求和。
六、乘公比错项相减(等差×等比)
乘公比错项相减法实际上是错位相减法的一种特例,专门用于求解等差数列与等比数列相乘形式的数列和。通过乘以公比并错位相减,可以有效求解此类数列的前$n$项和。
七、迭代法(或称为叠加法)
迭代法主要用于处理数列的递推关系,即数列的每一项与前一项或前几项有关。当数列满足$a_{n+1} = a_n + f(n)$,且$f(n)$是等差或等比数列时,可以通过迭代关系逐步求解数列的每一项,进而求和。这种方法在求解复杂数列的通项公式和前$n$项和中非常有用。
综合应用与注意事项
在实际应用中,这七种方法往往需要根据数列的具体形式灵活选择。对于简单的等差数列和等比数列,直接使用公式法是最快捷的方法。而对于复杂数列,则可能需要结合分组求和、裂项相消、错位相减等多种方法综合运用。
此外,在解题过程中还需注意以下几点:
1. 明确数列类型:首先分析数列是否为等差数列、等比数列或其他类型的数列,以选择合适的求和方法。
2. 公式适用范围:使用公式法时,要确保数列满足公式的适用条件,避免错误应用。
3. 验证结果:求和完成后,可通过验算或逻辑推断验证结果的正确性。
综上所述,数列求和的七种方法各有特点,掌握并灵活运用这些方法,对于提高数学解题能力和思维水平具有重要意义。希望本文的介绍能够帮助读者更好地理解和应用这些数列求和技巧。
- 上一篇: 揭秘!冒号背后隐藏的深意:它究竟代表了什么?
- 下一篇: 常见的'里'字组词有哪些呢?
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/03
-
03/03
-
03/03
-
03/03
-
03/03









