揭秘二项式公式的奥秘：定义、应用与详解

在数学的浩瀚宇宙中，二项式公式犹如一颗璀璨的星辰，它不仅照亮了组合数学的道路，也深刻影响着代数学、概率论等多个学科领域。当我们谈及“二项式公式是什么”这一命题时，实际上是在探索一个既古老又常新的数学工具，它以一种优雅而强大的方式，揭示了多项式乘法背后的深刻规律。

二项式公式的起源与定义

二项式公式，又称二项式定理（Binomial Theorem），最早可追溯至古希腊数学家欧几里得（Euclid）的著作中，但真正形成完整理论并广泛流传的，则是归功于文艺复兴时期的数学家帕斯卡（Pascal）和中国宋代数学家杨辉。这个定理描述的是，一个二项式（形如(a+b)^n）展开后各项系数之间的规律，其中n为正整数。

具体来说，二项式定理可以表示为：

\[

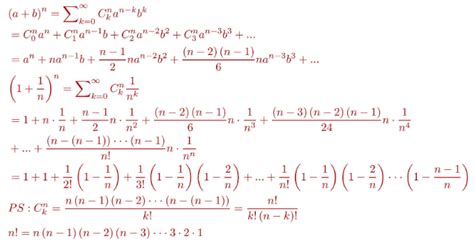
(a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k

\]

其中，\(\binom{n}{k}\)表示组合数，即从n个不同元素中取出k个元素的组合方式数，也常写作C(n,k)或nCk，计算公式为\(\frac{n!}{k!(n-k)!}\)，其中n!表示n的阶乘，即n×(n-1)×...×2×1。这个公式揭示了，当我们将两个数的和进行n次幂运算时，其结果可以表示为一系列项的和，每一项都是这两个数的幂的乘积，而系数则由组合数决定。

二项式公式的应用与意义

二项式公式不仅仅是一个数学上的定理，它在多个领域都有着广泛的应用和深远的影响。

1. 代数简化：最直接的应用就是简化了多项式的乘法运算。通过二项式定理，我们可以迅速展开形如(a+b)^n的表达式，避免了繁琐的乘法分配律应用，大大提高了计算效率。

2. 组合数学：二项式系数\(\binom{n}{k}\)本身就是组合数学的核心概念之一，它代表了从n个不同元素中选取k个元素的组合方式数。因此，二项式定理为研究组合计数问题提供了强有力的工具。

3. 概率论与统计学：在概率论中，二项式分布是一个重要的离散概率分布，它描述了在固定次数的独立重复试验中，某一事件恰好发生特定次数的概率。而二项式定理正是这一分布背后数学原理的基石。

4. 微积分与级数展开：在微积分学中，当a或b趋近于0时，二项式定理可以用于将某些函数展开为无穷级数，这对于函数的近似计算、泰勒级数展开等都有着重要意义。

5. 物理学与工程学：在物理学和工程学的众多领域中，二项式公式也扮演着重要角色。例如，在电路分析中，二项式定理可用于简化复杂的电路表达式；在力学中，它可用于求解特定条件下的振动问题。

深入理解二项式公式的本质

二项式公式的魅力不仅在于其实用性，更在于其背后所蕴含的深刻数学思想。它揭示了代数结构与组合数学之间的紧密联系，展示了数学内部不同分支之间的和谐统一。通过二项式定理，我们可以更加深刻地理解幂运算的本质，以及幂运算中各项系数与组合数之间的内在联系。

此外，二项式公式还蕴含着丰富的数学美。当我们将二项式定理的展开式写出来时，那些按照一定规律排列的系数构成了一个美丽的数学图案——帕斯卡三角形（也称杨辉三角）。这个三角形不仅揭示了组合数的递推关系，还展示了数学中的对称性和递归性，是数学美学的一个绝佳例证。

结语

综上所述，“二项式公式是什么”这一问题，实际上是在探索一个跨越多个数学领域、具有广泛应用和深刻数学思想的定理。它不仅是代数学中的一个重要工具，更是连接代数、组合数学、概率论等多个数学分支的桥梁。通过深入学习二项式公式，我们不仅可以提高解决具体数学问题的能力，更可以领略到数学之美的无穷魅力。在未来的学习和研究中，让我们继续探索二项式公式的奥秘，感受数学的无穷魅力吧！