扇形面积的计算公式是什么?
在浩瀚的数学宇宙中,隐藏着无数神秘而优雅的公式,它们如同星辰般点缀着人类智慧的夜空。今天,就让我们踏上一场探索之旅,揭开一个既古老又充满魅力的数学谜题——“扇形公式”的秘密面纱。这不仅仅是一次公式的简单介绍,更是一场关于形状、比例与计算的美妙邂逅,保证让你在享受知识盛宴的同时,也能感受到数学的独特魅力。
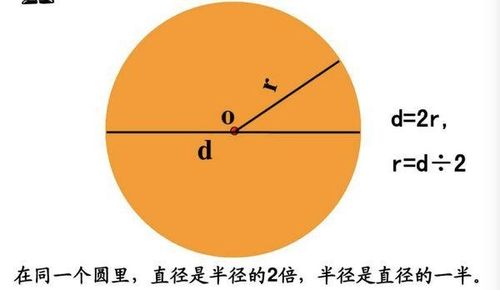
扇形:圆中的艺术切片
想象一下,你手中拿着一枚精致的圆饼,轻轻一刀,从圆心出发,优雅地划过一道弧线,于是,一块完美的扇形便呈现在了你的眼前。扇形,这个由圆心和两条半径以及它们之间的一段弧所围成的图形,不仅是几何学中的基础元素,更是自然界与设计中常见的灵感源泉。从花朵的绽放、贝壳的曲线到古老建筑的穹顶,扇形无处不在,以其独特的形态诉说着对称与和谐的美。
扇形公式的奥秘之门
那么,这个看似简单的图形背后,究竟隐藏着怎样的数学奥秘呢?答案就藏在“扇形公式”之中。扇形公式,顾名思义,是用来描述扇形面积或弧长等属性的数学表达式。它不仅是我们计算扇形相关量的钥匙,更是连接几何直观与数学抽象的桥梁。
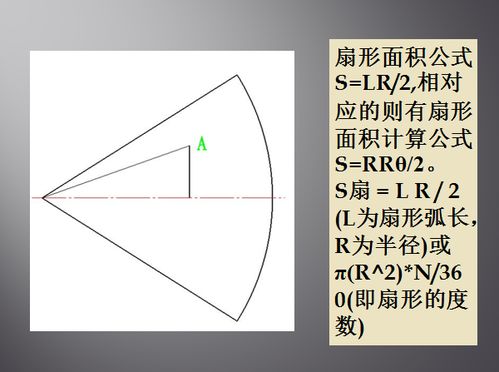
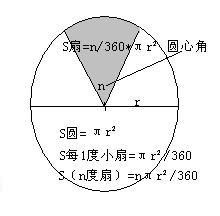
扇形面积公式:解锁空间之秘
首先,让我们聚焦于扇形面积的计算。想象一下,如果你知道整个圆的面积和扇形的圆心角,那么你能否计算出扇形的面积呢?答案是肯定的!扇形面积公式就是这一问题的完美解答:
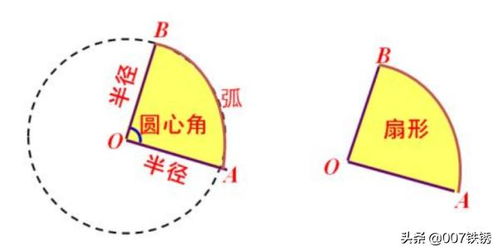
\[ \text{扇形面积} = \frac{\theta}{360} \times \pi r^2 \]
其中,\(\theta\) 是扇形的圆心角(以度为单位),\(r\) 是圆的半径,\(\pi\) 是圆周率。这个公式告诉我们,扇形面积占整个圆面积的比例,正好等于其圆心角占整个圆周(360度)的比例。通过它,我们可以轻松地将一个复杂的几何问题转化为简单的比例计算,感受到数学中的简洁与和谐。
扇形弧长公式:丈量曲线之美
除了面积,扇形的弧长也是我们在实际应用中经常需要计算的一个量。想象一下,你沿着扇形的边缘走一圈,所走过的路径长度就是扇形的弧长。那么,如何计算这个长度呢?扇形弧长公式给出了答案:
\[ \text{扇形弧长} = \frac{\theta}{360} \times 2\pi r \]
这个公式与扇形面积公式有着异曲同工之妙,都是利用圆心角与圆周的比例关系来进行计算。不过,这次我们关注的是圆周上的一小段弧,而不是整个圆面。通过这个公式,我们得以用数字来量化曲线的长度,进一步加深了对扇形乃至整个几何世界的理解。
扇形公式的应用之旅
掌握了扇形公式,就如同拥有了一把探索世界的钥匙。它们的应用范围之广,超乎你的想象。从简单的日常生活到复杂的科学研究,扇形公式的身影无处不在。
建筑设计:在设计圆形穹顶或扇形窗户时,建筑师们需要利用扇形公式来确保结构的稳定性和美观性。
工程测量:工程师在进行桥梁、隧道等圆形结构的施工时,也需要借助扇形公式来计算所需材料的面积和弧长。
地理研究:在地理学中,扇形地形的分析往往涉及到扇形面积的计算,帮助科学家们了解地貌的形成和演变。
物理学:在旋转动力学中,扇形弧长的概念与角速度、角加速度等物理量紧密相连,是理解物体旋转运动规律的关键。
结语:数学之美,无处不在
通过这场对扇形公式的探索之旅,我们不难发现,数学并非枯燥无味的数字游戏,而是充满了美感和智慧的学科。扇形公式作为其中的一颗璀璨明珠,不仅揭示了圆形世界中的奥秘,更引导我们走进了一个充满想象和创造的空间。在未来的日子里,不妨继续保持着这份好奇心和探索欲,去发现更多数学之美,让知识的光芒照亮你前行的道路。
- 上一篇: 高效解决卫生间防水补漏的实用方法
- 下一篇: 冲的多音字有哪些常见组词及用法?
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/10
-
03/10
-
03/10
-
03/10
-
03/10









