如何计算扇形的弧长
在几何学的广阔天地里,扇形作为一个独特的图形,不仅承载着圆形与直线之间的美妙过渡,还蕴含着丰富的数学原理与计算方法。其中,扇形的弧长计算,作为这一领域内的基本问题之一,不仅在日常生活中有着广泛的应用,如设计扇形门窗、计算风扇叶片的周长等,更是深入学习微积分、三角函数等高级数学知识的基础。本文将从定义理解、公式推导、应用实例及解题技巧等多个维度,深入浅出地探讨扇形弧长的求解方法。
一、扇形的定义与基本属性
首先,让我们明确扇形的定义。扇形是圆的一部分,由两条半径和它们之间所夹的弧围成。这两条半径的夹角称为扇形的圆心角,它决定了扇形在圆中所占的比例。扇形的一个重要属性是其弧长,即围成扇形的那段圆的边缘的长度。
二、扇形弧长公式的推导
扇形弧长的计算依赖于圆周长的概念以及圆心角与整个圆周角(即360°或2π弧度)的比例关系。在正式推导公式之前,我们需要了解两个基础公式:
1. 圆的周长公式:C = 2πr,其中C代表圆的周长,r是圆的半径,π是一个常数,约等于3.14159。
2. 弧长与圆心角的关系:设扇形的圆心角为n°(或α弧度),整个圆的圆心角为360°(或2π弧度),则扇形弧长l与圆周长C之间的关系为:l = (n/360) × C 或 l = (α/2π) × C。
将圆的周长公式代入上述关系式中,得到扇形弧长的计算公式:
角度制下:l = (n/360) × 2πr = (nπr)/180
弧度制下:l = (α/2π) × 2πr = αr
这两个公式是求解扇形弧长的核心工具,适用于不同单位制下的圆心角表示。
三、应用实例
实例一:计算风扇叶片的周长
假设一个风扇的叶片形状近似为扇形,已知风扇的半径为20厘米,叶片占整个圆的圆心角为90°。我们需要计算这个风扇叶片的周长(即扇形弧长加上两条半径的长度)。
解:首先,根据扇形弧长公式,在角度制下,弧长l = (90π × 20)/180 = 10π厘米。然后,加上两条半径的长度,即2 × 20 = 40厘米。所以,风扇叶片的周长约为10π + 40 ≈ 62.83厘米(取π ≈ 3.14)。
实例二:设计扇形门窗
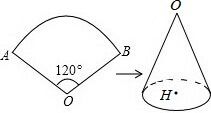
在设计一扇扇形门窗时,设计师需要知道扇形的弧长以确定所需的材料长度。假设门窗的半径为1米,且希望其打开的圆心角为120°。
解:直接应用扇形弧长公式,在角度制下,弧长l = (120π × 1)/180 = (2π)/3米。这样,设计师就能准确地计算出所需材料的长度。
四、解题技巧与注意事项
1. 单位统一:在计算过程中,确保圆心角的单位与所使用的公式单位制相匹配。若题目给出的是角度制,则使用(nπr)/180公式;若给出的是弧度制,则使用αr公式。
2. 精确计算与近似值:在计算过程中,π的取值可根据需要选择精确值或近似值。在要求精度不高的场合,可取π ≈ 3.14进行计算;在需要高精度的场合,则应使用更精确的π值或利用计算器进行计算。
3. 理解与应用:深入理解扇形弧长公式的推导过程,有助于更好地掌握其应用。通过多做练习,将理论知识与实际问题相结合,提高解题能力。
4. 注意扇形的完整性:在计算扇形弧长时,要注意扇形的完整性,即它是由两条半径和一条弧组成的。在某些问题中,可能需要同时考虑弧长和半径的长度。
结语
扇形弧长的计算,作为几何学中的一个基础而重要的知识点,不仅加深了我们对圆与直线之间关系的理解,还为后续学习更复杂的数学知识奠定了基础。通过本文的阐述,希望读者能够掌握扇形弧长的计算方法,并能在实际生活中灵活运用,解决实际问题。同时,也期待读者能在不断探索与实践中,发现更多数学之美,享受学习数学的乐趣。
- 上一篇: 从S速升级到M速:一键优化你的手机网络秘籍!
- 下一篇: 揭秘:鸡胗究竟是何物?带你深入了解!
新锐游戏抢先玩
游戏攻略帮助你
更多+-
01/31
-
01/31
-
01/31
-
01/31
-
01/31









