揭秘！轻松学会圆柱体体积的神奇计算法

在日常生活和学习中，我们经常会遇到各种形状的物体，其中圆柱体是一种常见的几何体。它像一根笔直的管子，上下底面都是完全相同的圆，侧面则是一个曲面。当我们需要知道一个圆柱体里面能装多少东西，或者它的空间占有多大时，就需要计算它的体积。那么，圆柱体的体积到底怎么计算呢？下面，我们就用简单易懂的方式来聊聊这个话题。

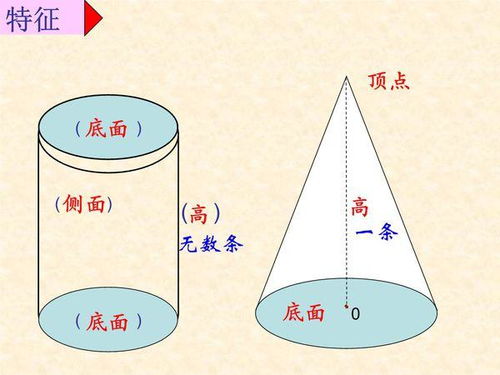
一、认识圆柱体

首先，让我们再次明确一下什么是圆柱体。想象一个圆柱形的水杯，它有一个圆形的底部，一个同样大小的圆形顶部，以及连接这两个圆面的曲面侧壁。这个结构就构成了一个圆柱体。圆柱体的主要特征包括：两个平行的、大小相同的圆形底面，以及一个侧面，侧面展开后通常是一个矩形（当圆柱体垂直放置时）。

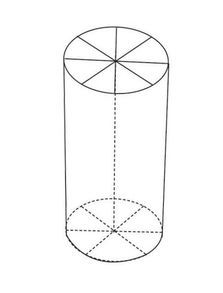
二、圆柱体体积的概念

体积，简单来说，就是一个物体占据的空间大小。对于圆柱体而言，它的体积就是它内部能容纳物质的总量。计算圆柱体的体积，就是找出这个“管子”里面到底有多少“空间”。

三、圆柱体体积的计算公式

要计算圆柱体的体积，我们需要用到一个非常重要的公式，那就是：

圆柱体的体积 = 圆的面积 × 圆柱体的高

这里，“圆的面积”指的是圆柱体底面的面积，而“圆柱体的高”则是从上底面到下底面的垂直距离。

1. 圆的面积怎么计算？

在继续之前，我们先快速回顾一下圆的面积计算公式，因为我们需要用到它来计算圆柱体的体积。圆的面积计算公式是：

圆的面积 = π × 半径²

其中，“π”是一个特殊的数，大约等于3.14159...，“半径”则是从圆心到圆上任意一点的距离。

2. 结合公式计算圆柱体体积

现在，我们已经知道了圆的面积如何计算，接下来就可以轻松地推导出圆柱体的体积公式了。将圆的面积公式代入到圆柱体体积的公式中，我们得到：

圆柱体的体积 = π × 半径² × 圆柱体的高

这个公式就是计算圆柱体体积的“金钥匙”。

四、实际操作：如何应用公式

假设我们有一个圆柱形的水杯，我们知道了它的底面半径是5厘米，高度是10厘米。现在，我们想知道这个水杯能装多少水，也就是它的体积是多少。

1. 确定参数：

半径 r = 5厘米

高度 h = 10厘米

π（这里我们取近似值）≈ 3.14

2. 代入公式：

将上述数值代入到圆柱体体积的公式中：

$$ \text{体积} = 3.14 \times 5^2 \times 10 $$

3. 进行计算：

首先计算半径的平方：$5^2 = 25$

然后乘以π和高度：$3.14 \times 25 \times 10 = 785$

4. 得出结果：

所以，这个圆柱形水杯的体积大约是785立方厘米。

五、注意事项与实际应用

精确度：在实际计算中，根据需要可以选择π的精确度。对于大多数日常应用，π取到小数点后两三位（如3.14）已经足够精确。

单位统一：在计算过程中，确保所有参与计算的量（如半径、高度）的单位是统一的，以避免出现错误。

实际应用：圆柱体体积的计算不仅限于水杯这样的简单例子。它在建筑、工程、科学实验等多个领域都有广泛应用，比如计算油罐的储油量、圆柱形管道内的流体量等。

六、结语

通过上面的讲解，相信你已经对如何计算圆柱体的体积有了清晰的认识。记住，关键在于掌握圆柱体体积的公式，并能灵活运用它来解决实际问题。无论是在学校的学习中，还是在日常生活中，这个技能都会给你带来很大的帮助。希望这篇文章能够激发你对几何学的兴趣，让你在探索几何世界的道路上越走越远！