secx的数学定义及表达式

在探索数学的浩瀚宇宙时，你是否曾被那些看似简单却蕴含着无限奥秘的符号所吸引？今天，就让我们一起揭开一个既熟悉又神秘的数学面纱——“secx 等于什么？”，这不仅仅是一个公式的追问，更是一场通往几何与三角学奇妙世界的旅行。

开篇：遇见secx，一场不期而遇的数学奇遇

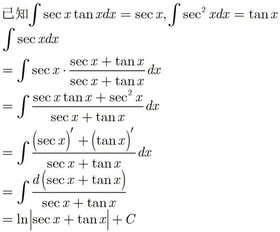
想象一下，你正漫步在一条由无数数学公式铺就的小径上，突然，一个身影从公式丛中跃出，它身披“secx”的徽章，眼神中闪烁着智慧的光芒，仿佛在邀请你进入一个全新的世界。这就是我们的主角——正割函数（secant function），简称secx。

初探：secx的庐山真面目

要理解secx，首先得从它的“家族”说起。在三角函数的大家庭里，secx与sin（正弦）、cos（余弦）、tan（正切）等成员并肩作战，共同解决了无数几何与物理问题。但与其他几位略显低调的兄弟不同，secx以其独特的定义和性质，成为了这个家族中一颗璀璨的明星。

定义揭晓：secx，全称为“正割函数”，其定义为“余弦函数的倒数”。简单来说，如果你知道某个角的余弦值cosθ，那么secθ就等于1除以cosθ，即secθ = 1/cosθ。这个定义听起来简单，却蕴含着深刻的几何意义和广泛的应用场景。

深入：secx的几何解释与图像之美

要真正理解secx，我们还需要从几何的角度去审视它。想象一个单位圆（半径为1的圆），secx的值实际上就是与x轴正方向夹角为θ的射线与x轴正方向之间的“距离”（注意，这里说的“距离”在数学上更准确地应该是“线段的长度”的倒数，因为当射线与x轴平行时，余弦值为0，secx将趋于无穷大）。这种解释让我们直观地感受到了secx与几何图形的紧密联系。

进一步地，我们可以绘制出secx的图像。不同于sin和cos函数的周期性波动，secx的图像呈现出一种独特的“无限增长”特性。当θ接近90度（或π/2弧度）时，cosθ趋于0，secθ则急剧增大，趋于正无穷；同理，当θ接近-90度时，secθ趋于负无穷。这种“爆炸性”的增长使得secx的图像在某些区域显得尤为引人注目。

应用：secx在现实世界中的身影

那么，如此独特的secx究竟有何用处呢？答案是多方面的。在物理学中，secx经常出现在力学、光学等领域的问题中，如求解斜面上的物体受力情况、光线通过介质时的折射问题等。在工程学中，secx则是设计斜坡、桥梁等结构时不可或缺的工具。此外，在三角测量、地图制作等领域，secx也发挥着重要作用。

拓展：secx与三角恒等式、导数的奇妙联动

值得一提的是，secx还与三角恒等式和导数有着千丝万缕的联系。通过三角恒等式，我们可以将secx与其他三角函数相互转化，从而简化复杂的数学问题。例如，利用“1 + tan²θ = sec²θ”这一恒等式，我们可以轻松地在secx、tanx和cosx之间建立联系。

而在微积分领域，secx的导数更是揭示了其内在的动态变化规律。通过计算可知，secx的导数为secx·tanx，这一结果不仅加深了我们对secx性质的理解，还为我们解决更复杂的数学问题提供了有力工具。

结语：secx，数学之美的缩影

回望我们的探索之旅，从secx的定义出发，我们穿越了几何与三角学的广阔天地，见证了secx在现实世界中的广泛应用，更感受到了它与三角恒等式、导数等数学概念的深刻联系。secx，这个看似简单的数学符号，实则蕴含了丰富的数学思想和无尽的智慧。

在未来的数学探索中，或许你还会遇到更多像secx这样的“数学精灵”，它们将引领你走进一个又一个充满惊喜的数学世界。让我们带着对数学的热爱和好奇，继续前行在这条无尽的探索之路上吧！