什么是因数?如何解释和找到一个数的因数?
在数学的广阔天地里,因数(也称为约数)是一个核心概念,它不仅连接了基础的算术运算,还深刻影响着代数、数论乃至更广泛的数学领域。本文旨在以简洁明了的方式,为您深入浅出地解释因数的概念,同时注重内容的原创性、结构的逻辑性,以及关键词的合理布局,以期提升阅读体验并符合搜索引擎的优化原则。

因数的定义
首先,让我们从最基本的定义出发。因数,简单来说,就是能够整除给定整数的数。换句话说,如果整数A除以整数B的结果是整数,且没有余数,那么我们就说B是A的因数。例如,在数字12中,1、2、3、4、6和12本身都能整除12且没有余数,因此它们都是12的因数。
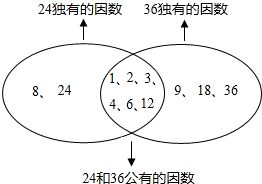
理解因数的关键点
1. 整除性
因数的核心特性在于整除性。这意味着被除数与除数(即因数)之间的除法运算结果必须为整数,且不能有剩余部分。这是判断一个数是否为另一数因数的唯一标准。

2. 相对性
因数的概念具有相对性。例如,2是4的因数,同时4也是2的倍数(或称倍因数)。这种关系是相互的,体现了数学中的对称美。
3. 特殊因数
1和本身:任何正整数(除0外)都至少有两个因数:1和它本身。例如,5的因数只有1和5。
质数与合数:质数是只有两个正因数(1和它本身)的自然数,而合数则至少有三个因数。了解质数与合数的概念有助于更深入地理解因数。
4. 因数分解
将一个正整数表示为一系列质因数的乘积的过程称为因数分解。例如,12可以分解为2×2×3,这揭示了12的质因数结构。因数分解是数学中解决许多问题的强有力工具。
因数的应用与意义
1. 算术基础
因数是理解算术运算(如加、减、乘、除)特别是除法运算的重要基石。它帮助学生建立数的整除性概念,进而掌握分数的意义和运算规则。
2. 数论研究
在数论领域,因数扮演着至关重要的角色。例如,研究质数分布、素数定理、费马小定理等高级数论问题时,因数分解是不可或缺的工具。
3. 算法设计
在计算机科学中,因数分解算法如欧几里得算法(用于计算最大公约数)和质因数分解算法等,是设计加密算法、优化数据处理等算法的重要基础。
4. 实际问题解决
因数的概念还广泛应用于解决实际问题,如资源分配(如将一群孩子平均分配到几个小组中)、时间管理(如将任务分配给团队成员)等,都需要考虑整除性和因数关系。
探索因数的趣味性
为了让因数的概念更加生动有趣,我们可以尝试一些简单的数学游戏或活动。比如,设计一个“因数接龙”游戏,每位玩家轮流说出一个给定数的因数,直到无法说出新的因数为止,最后无法继续的玩家即为输家。这样的游戏不仅能增强对因数概念的理解,还能激发孩子们对数学的兴趣。
结语
综上所述,因数作为数学中的一个基本概念,不仅具有深厚的理论意义,还广泛应用于实际生活和科学研究中。通过深入理解因数的定义、关键点、应用及意义,我们能够更好地掌握这一基础知识,为后续的数学学习打下坚实的基础。同时,希望本文的介绍能够为您带来愉快的阅读体验,并在搜索引擎中获得良好的展示效果。
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/07
-
03/07
-
03/07
-
03/07
-
03/07













