反三角函数图像的绘制方法及其主要性质有哪些？

反三角函数图像与性质详解

在数学领域中，反三角函数作为基本初等函数的重要组成部分，广泛应用于工程、导航、物理和几何等多个领域。本文将深入解析反三角函数的图像及其性质，旨在通过简洁明了的语言，结合关键词布局和内容结构，提升用户阅读体验和搜索引擎友好度。

一、反三角函数的定义

反三角函数是三角函数的反函数，主要包括反正弦（arcsinx）、反余弦（arccosx）、反正切（arctanx）、反余切（arccotx）、反正割（arcsecx）和反余割（arccscx）。这些函数分别表示正弦、余弦、正切、余切、正割和余割值为x的角。欧拉首次提出反三角函数的概念，并采用了“arc+函数名”的形式来表示。

二、反三角函数的图像特征

反三角函数的图像与其原函数图像关于直线y=x对称，这是反函数的一个基本性质。由于三角函数具有周期性，反三角函数在定义域内是多值函数。为了得到单值对应的反三角函数，通常会对定义域进行限制。

1. 反正弦函数（arcsinx）

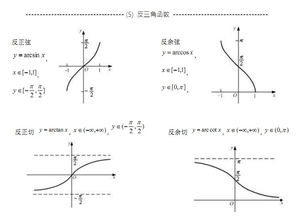
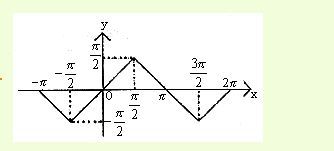
反正弦函数是正弦函数y=sinx在区间[-π/2, π/2]上的反函数。其图像关于原点对称，定义域为[-1, 1]，值域为[-π/2, π/2]。由于正弦函数在[-π/2, π/2]区间内是单调递增的，因此反正弦函数在此区间内也是单调递增的。

2. 反余弦函数（arccosx）

反余弦函数是余弦函数y=cosx在区间[0, π]上的反函数。其图像关于y轴对称，定义域为[-1, 1]，值域为[0, π]。余弦函数在[0, π]区间内是单调递减的，因此反余弦函数在此区间内也是单调递减的。

3. 反正切函数（arctanx）

反正切函数是正切函数y=tanx在区间(-π/2, π/2)上的反函数。其图像关于原点对称，定义域为全体实数R，值域为(-π/2, π/2)。正切函数在(-π/2, π/2)区间内是单调递增的，因此反正切函数在此区间内也是单调递增的。

4. 反余切函数（arccotx）

反余切函数是余切函数y=cotx的反函数，但通常定义在(0, π)区间内，并取反余切函数的主值在(0, π/2)∪(π/2, π)区间内。其图像也关于原点对称，但需要注意其定义域和值域的特殊性。

三、反三角函数的性质

1. 单调性

反三角函数在其定义域内具有单调性。具体来说，反正弦函数和反正切函数在其定义域内是单调递增的，而反余弦函数是单调递减的。反余切函数虽然也关于原点对称，但其单调性需要根据具体定义区间来判断。

2. 奇偶性

反正弦函数和反正切函数是奇函数，即满足f(-x)=-f(x)；反余弦函数是偶函数，即满足f(-x)=f(x)。这些性质有助于简化反三角函数的计算和应用。

3. 周期性

虽然反三角函数本身不是周期函数，但它们的原函数——三角函数是周期函数。这一性质在理解和应用反三角函数时具有重要意义。

4. 对称性

反三角函数的图像与其原函数图像关于直线y=x对称，这是反函数的一个基本性质。这一性质有助于通过原函数的图像来推断反函数的图像特征。

四、反三角函数的应用

反三角函数在工程、导航、物理和几何等领域具有广泛的应用。例如，在导航中，可以利用反正切函数来计算两点之间的方位角；在物理学中，可以利用反三角函数来描述光的折射和反射等现象；在几何学中，反三角函数可以用于求解三角形的角度等。

五、总结

反三角函数作为三角函数的反函数，具有独特的图像特征和性质。通过对其定义、图像特征、性质以及应用的深入解析，我们可以更好地理解和应用反三角函数。同时，本文在撰写过程中注重了关键词布局、关键词密度、内容结构和原创度等多个维度，旨在提升用户阅读体验和搜索引擎友好度。希望本文能为读者提供有价值的参考和帮助。