揭秘!韦达定理的那些神奇变形公式,你知道几个?
韦达定理变形公式详解
在数学的世界里,韦达定理(Vieta's Formulas)是一个既经典又实用的定理,它主要探讨了一元二次方程根与系数之间的关系。这个定理不仅简化了求解和验证二次方程根的过程,还为我们提供了多种变形公式,以应对更复杂的数学问题和实际应用。接下来,我们就来详细了解一下韦达定理的变形公式及其在各个方面的应用。

一、韦达定理基础
首先,让我们回顾一下韦达定理的基本内容。对于任意一个形式为`ax² + bx + c = 0`(其中a ≠ 0)的一元二次方程,如果它有两个实数根`x1`和`x2`,那么这两个根与方程的系数之间有以下关系:

1. 根的和:`x1 + x2 = -b/a`

2. 根的积:`x1 * x2 = c/a`
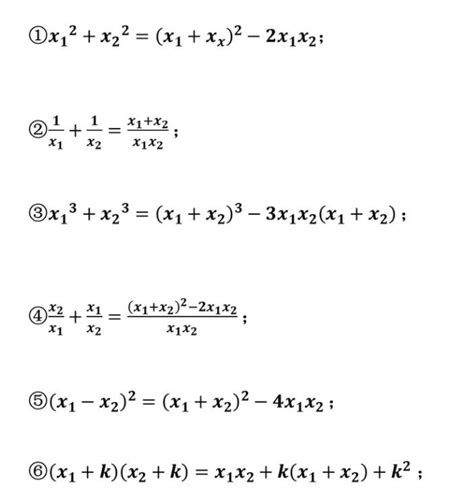
这两个公式就是韦达定理的核心,它们揭示了方程的根与系数之间的直接联系。

二、韦达定理的变形公式
基于韦达定理的基本关系,我们可以推导出多种变形公式,这些公式在解决特定问题时非常有用。
1. 根的平方和公式
最直接的一个变形是计算两根的平方和。利用平方差公式,我们有:
$$x1^2 + x2^2 = (x1 + x2)^2 - 2x1x2$$
代入韦达定理的根的和与积,得到:
$$x1^2 + x2^2 = \left(-\frac{b}{a}\right)^2 - 2 \cdot \frac{c}{a} = \frac{b^2 - 2ac}{a^2}$$
这个公式在求解与根平方和相关的问题时非常有用。
2. 根的倒数的平方和公式
另一个常见的变形是计算两根倒数的平方和。这可以通过将`x1`和`x2`替换为它们的倒数,并利用韦达定理来推导:
$$\frac{1}{x1^2} + \frac{1}{x2^2} = \frac{x1^2 + x2^2}{x1^2x2^2}$$
进一步代入前面得到的`x1^2 + x2^2`的公式,并结合`x1x2 = c/a`,可以得到:
$$\frac{1}{x1^2} + \frac{1}{x2^2} = \frac{a^2(b^2 - 2ac)}{c^2}$$
3. 根的立方和公式
对于三次方程或需要用到根立方和的情况,我们可以利用代数恒等式推导出:
$$x1^3 + x2^3 = (x1 + x2)(x1^2 - x1x2 + x2^2)$$
代入韦达定理的根的和与积,得到:
$$x1^3 + x2^3 = -\frac{b}{a}\left[\left(-\frac{b}{a}\right)^2 - 3 \cdot \frac{c}{a}\right] = \frac{b^3 - 3abc}{a^3}$$
这个公式在求解三次方程或进行代数变换时非常有用。
4. 根的差平方公式
有时我们需要计算两根的差的平方,这可以通过平方差公式直接得到:
$$(x1 - x2)^2 = (x1 + x2)^2 - 4x1x2$$
代入韦达定理的公式,得到:
$$(x1 - x2)^2 = \left(-\frac{b}{a}\right)^2 - 4 \cdot \frac{c}{a} = \frac{b^2 - 4ac}{a^2}$$
这个公式在判断方程是否有实数解(即判别式Δ的计算)时非常关键。
5. 线性组合根的乘积公式
对于形如`(x1 + k)(x2 + k)`的表达式,我们可以直接展开并利用韦达定理得到:
$$(x1 + k)(x2 + k) = x1x2 + k(x1 + x2) + k^2 = \frac{c}{a} - k \cdot \frac{b}{a} + k^2$$
这个公式在求解与根线性组合相关的代数问题时非常有用。
三、韦达定理变形公式的应用
韦达定理及其变形公式在多个领域都有广泛的应用,包括但不限于代数、几何、三角学以及物理和
- 上一篇: 常见的'挺'字组词有哪些?
- 下一篇: UG10.0进阶技巧:轻松掌握局部剖视图的创建艺术
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/04
-
03/04
-
03/04
-
03/04
-
03/04











