揭秘！正交矩阵的八大迷人性质，你了解几个？

在深入探讨正交矩阵这一数学概念的性质时，我们不可避免地会被其独特的几何与代数特性所吸引。正交矩阵，作为线性代数中的一类重要矩阵，不仅在理论研究中占据核心地位，而且在工程、物理、计算机科学等多个领域都有广泛应用。本文将从定义出发，逐步展开对正交矩阵性质的探讨，涵盖其几何意义、代数特征、与其他矩阵变换的关系，以及在实际问题中的应用等多个维度。

一、正交矩阵的定义与直观理解

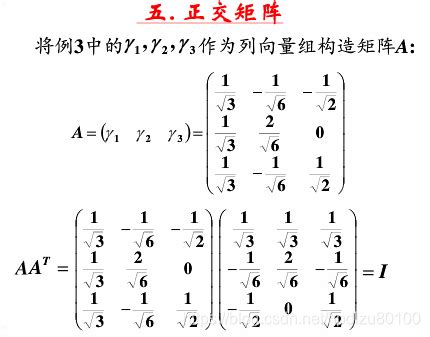
定义回顾：正交矩阵是指其行向量和列向量都是单位向量且两两正交的方阵。在数学上，若矩阵$Q$满足$Q^TQ = QQ^T = I$（其中$I$为单位矩阵），则称$Q$为正交矩阵。这里的“正交”一词源自向量的正交性，即两个向量的点积为零，且两者均为单位长度时，称这两个向量为正交单位向量。

直观理解：从几何角度来看，正交矩阵代表了一种“不改变形状但可能改变方向”的线性变换。想象在二维或三维空间中，通过正交矩阵变换，任何向量都将保持其长度不变（即模长不变），而仅仅可能改变其方向。这种变换在保持向量间相对角度（即正交性）的同时，也保持了空间的度量性质（如距离）。

二、正交矩阵的代数特征

行列式性质：由于正交矩阵的列（行）向量均为单位长度且相互正交，其行列式（Determinant）的绝对值必为1。这意味着正交变换保持了空间的定向性，即左手系变换后仍为左手系，右手系则保持为右手系。

特征值与特征向量：正交矩阵的所有特征值（Eigenvalues）的模均为1，且其对应的特征向量（Eigenvectors）之间也是正交的。这一性质使得正交矩阵在求解特征值和特征向量时具有独特的优势，尤其是在处理物理和工程中的振动、稳定性等问题时尤为重要。

逆矩阵与转置：正交矩阵的一个重要性质是其逆矩阵等于其转置矩阵，即$Q^{-1} = Q^T$。这一性质极大地简化了计算，因为求逆过程仅需进行矩阵转置，无需执行复杂的行列式或伴随矩阵运算。

三、正交矩阵与几何变换

旋转与反射：在二维和三维空间中，正交矩阵可以表示旋转和（或）反射变换。例如，二维空间中的旋转矩阵就是一个典型的正交矩阵，它围绕原点旋转向量而不改变其长度。三维空间中的正交矩阵则可以表示围绕某条过原点的轴的旋转，或是通过某个平面的反射。

坐标变换：在坐标系变换中，正交矩阵用于将一组坐标基转换为另一组正交坐标基。这种变换在物理学、工程学中常用于简化问题的求解，如通过选择合适的坐标系来消除方程中的某些项，从而使问题更容易处理。

四、正交矩阵在优化与算法中的应用

梯度下降与优化：在优化算法中，特别是当目标函数为二次型时，使用正交矩阵作为变换矩阵可以简化问题，因为正交变换不会改变向量的模长和相对角度，从而保持了梯度下降过程中的几何特性。此外，在正则化方法中，通过正交矩阵进行变换可以更容易地实现某些特定的约束条件。

信号处理与图像处理：在信号处理和图像处理领域，正交变换（如傅里叶变换、离散余弦变换等）广泛应用，它们的核心思想就是利用正交矩阵的特性来分解信号或图像，以便于分析、压缩或去噪。这些变换不仅保留了信号或图像的重要特征，还通过正交性去除了冗余信息，提高了处理效率。

五、总结与展望

正交矩阵以其独特的性质在多个领域发挥着不可替代的作用。从几何变换的直观理解到代数特征的深入剖析，再到在优化算法、信号处理等领域的广泛应用，正交矩阵展现了其强大的数学魅力和实用价值。未来，随着科学技术的不断发展，正交矩阵及其相关理论的研究将继续深入，为更多领域的创新与发展提供有力支持。

总之，正交矩阵作为线性代数中的一个重要概念，其性质丰富多样，应用广泛深远。通过对这些性质的深入学习和理解，我们不仅能够更好地掌握线性代数的核心知识，还能够将这些知识灵活应用于实际问题的解决中，从而推动科学技术的进步与发展。