轻松掌握:分数乘除法的计算方法与技巧
分数的乘除法怎么算
在学习数学的道路上,分数的乘除法是一个既基础又关键的知识点。它不仅在日常生活中有所应用,更是后续学习代数、几何等高级数学内容的基础。下面,我们将通过简洁明了的步骤,帮助大家掌握分数的乘除计算方法,让复杂的问题变得一目了然。

一、分数的乘法
1. 理解基本概念
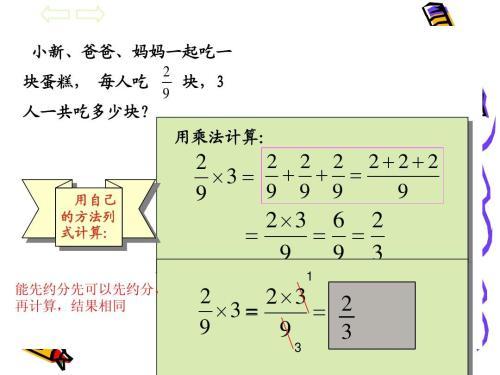
首先,我们要明确分数的定义:分数表示整体的一部分,由分子(分数线上的数)和分母(分数线下的数)组成。例如,1/2表示一个整体被均分为两份,取其中的一份。

2. 乘法运算法则
分数的乘法运算法则相当直观:分子乘分子,分母乘分母。即,对于两个分数a/b和c/d,它们的乘积为(a×c) / (b×d)。
3. 示例解析
假设我们要计算1/2与3/4的乘积。
分子相乘:1×3=3
分母相乘:2×4=8
因此,1/2 × 3/4 = 3/8。
4. 简化结果
在得到乘积后,如果可能,我们应该对分数进行简化。简化分数的方法是找出分子和分母的最大公约数(GCD),并用分子和分母分别除以这个GCD。但在此例中,3/8已经是最简形式,无需进一步简化。
5. 注意事项
当分子或分母为1时,乘法操作相对简单。例如,任何数与1/1(即1)相乘都等于它本身。
在计算过程中,如果得到的分子或分母很大,考虑先找公共因子进行约分,以避免计算过程中数字过于庞大。
二、分数的除法
1. 转换为乘法
分数的除法其实可以转化为乘法来简化计算。具体方法是:“除以一个数等于乘以这个数的倒数”。例如,a/b ÷ c/d 可以转化为 a/b × d/c。
2. 求倒数
一个数的倒数是1除以这个数。对于分数而言,其倒数就是分子分母互换位置。例如,(c/d)的倒数是d/c。
3. 应用乘法法则
将除法转化为乘法后,按照分数乘法的法则进行计算。即,先分子乘分子,再分母乘分母。
4. 示例解析
计算2/3 ÷ 4/5。
首先,将除法转化为乘法:2/3 ÷ 4/5 = 2/3 × 5/4。
应用乘法法则:分子相乘 2×5=10,分母相乘 3×4=12。
因此,2/3 ÷ 4/5 = 10/12。
简化结果:10和12的最大公约数是2,所以约分后得到5/6。
5. 注意事项
在进行除法转化为乘法的过程中,确保正确计算了除数的倒数。
简化结果是必要的步骤,它可以帮助我们得到最简洁的答案。
当遇到混合数(带分数)的除法时,先将带分数转化为假分数(即分子大于分母的分数),再进行上述操作。
三、总结
分数的乘除法虽然初看起来有些复杂,但只要掌握了基本的运算法则和技巧,就能轻松应对。无论是乘法中的“分子乘分子,分母乘分母”,还是除法中的“除以一个数等于乘以这个数的倒数”,都是解题的关键。此外,适时地对结果进行简化,也是获得正确答案的重要一环。希望通过这篇文章,大家能对分数的乘除法有一个更清晰、更全面的认识,并在实际解题中灵活运用。
- 上一篇: 轻松掌握!如何个性化设置微信服务通知提醒
- 下一篇: 如何有效培养小宝宝的忍耐力与自我控制能力?
游戏攻略帮助你
更多+-
04/13
-
04/13
-
04/13
-
04/13
-
04/13









