解答疑惑:分数的乘除法计算全攻略,轻松学会怎么算!
在我们日常生活的数学学习中,分数是一个既常见又实用的概念,它帮助我们更精确地描述部分与整体的关系。当我们遇到分数的乘除运算时,可能会觉得有些复杂,但其实只要掌握了基本规则,就能轻松应对。接下来,我们就一步步来揭开分数乘除法的神秘面纱,让这个过程变得既简单又有趣。
一、认识分数
首先,我们来回顾一下分数的基本概念。分数由两部分组成:分子和分母,它们之间用一条短线(分数线)隔开。比如,1/2就是一个分数,其中1是分子,表示我们要的部分数量;2是分母,表示整体被分成的等份数。简单来说,分数就是“部分”与“整体”的关系表示。

二、分数的乘法
1. 乘法的基本规则
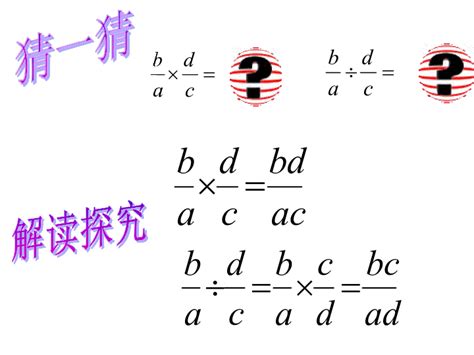
分数的乘法其实非常直观,我们可以把它想象成两个“部分”的结合。具体做法是:分子乘分子作为结果的分子,分母乘分母作为结果的分母。

例子:计算 2/3 × 1/4
分子相乘:2 × 1 = 2
分母相乘:3 × 4 = 12
所以,2/3 × 1/4 = 2/12
但通常我们会进一步化简分数,使其变得更简洁。在这个例子中,2/12可以化简为1/6(因为2和12都可以被2整除)。
2. 乘法的小技巧
约分:在乘法运算前,先观察两个分数的分子和分母是否有公因数,如果有,可以先约分,再进行计算,这样可以减少计算量。
交叉相乘:这是一个形象的说法,实际上就是指分子乘分子,分母乘分母。
理解意义:分数的乘法可以理解为“整体的部分再取部分”。比如,吃了一个蛋糕的2/3,再从这2/3中吃掉1/4,那么总共吃掉的部分就是2/3的1/4。
三、分数的除法
1. 转换为乘法
分数的除法其实并不复杂,我们可以利用“除以一个数等于乘以这个数的倒数”的原则,将除法转化为乘法。倒数就是分子和分母交换位置的分数,比如4/5的倒数是5/4。
例子:计算 2/3 ÷ 1/4
将除法转化为乘法:2/3 × (1/4的倒数)
求1/4的倒数:1/4 → 4/1
进行乘法运算:2/3 × 4/1 = 8/3
注意,这里的结果8/3已经是一个最简分数,无需再化简。
2. 除法的小技巧
记住倒数:熟练掌握一些常见分数的倒数,比如1/2的倒数是2,1/3的倒数是3/1(也就是3),可以大大提高计算速度。
避免复杂分数:在计算过程中,尽量保持分子和分母为整数或易于处理的数,避免产生过于复杂的分数。
检查答案:在得出答案后,不妨用小数或百分比验证一下,看看是否合理,这有助于我们发现和纠正错误。
四、实际应用
分数的乘除法不仅仅停留在纸面上,它们在生活中有着广泛的应用。比如:
烹饪:在烘焙或烹饪时,经常需要按比例调整食材的用量,这时分数的乘除法就显得尤为重要。
购物:打折促销时,商品的折扣往往以分数的形式出现,比如“打五折”就是乘以1/2,了解这一点能帮助我们快速计算出折扣后的价格。
时间管理:在处理时间相关的问题时,比如计算一个任务所需时间的比例,分数的乘除法也是不可或缺的工具。
五、总结
通过上述的介绍,我们可以看到,分数的乘除法其实并不复杂,只要掌握了基本规则和小技巧,就能轻松应对。无论是学习中的练习,还是生活中的实际应用,分数乘除法都是一项非常实用的技能。希望这篇文章能够帮助你更好地理解分数的乘除法,让你在数学的道路上越走越远,享受数学带来的乐趣。记住,多练习是提高计算能力的关键,不妨找些题目来练练手,相信你会越来越熟练!
新锐游戏抢先玩
游戏攻略帮助你
更多+-
01/31
-
01/31
-
01/31
-
01/31
-
01/31













