如何精确计算并应用黄金比例
在探讨“黄金比例”这一古老而迷人的数学概念时,我们首先要理解其核心——它不仅仅是一个简单的数值或比例,更是自然界与艺术创作中频繁出现的和谐之美的象征。黄金比例,又称黄金分割率,是一个约为0.6180339887...的无限不循环小数,通常用希腊字母φ(phi)表示,其精确值定义为(√5+1)/2。本文将深入浅出地介绍黄金比例的计算方法、应用场景及其背后的美学与数学原理,旨在为读者提供一个既易于理解又富有启发性的视角。
一、黄金比例的基本定义
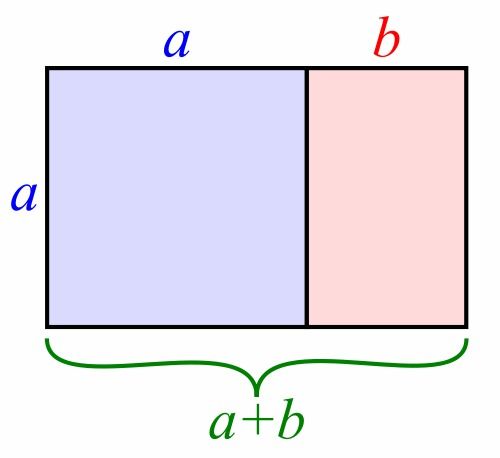
黄金比例是指将某一线段分为两部分,使较长部分与整体之比等于较短部分与较长部分之比,即a/b = (a+b)/a,其中a为较长部分,b为较短部分。解这个方程,我们得到φ ≈ 0.618或1/φ ≈ 0.618的互补比例。这一比例因其独特的和谐美感,在自然界、建筑、艺术、设计乃至科学研究等多个领域中被广泛应用和推崇。
二、黄金比例的计算方法
1. 几何作图法
最直观的计算黄金比例的方法之一是通过几何作图。一种经典的方法是使用圆和直线来构造。步骤如下:
画一个圆,并在圆上任取一点A作为起点。
从A点引出圆的切线,并在切线上选择一点B(非圆心),连接AB并延长至与圆相交于点C。
以B为圆心,BC为半径画圆,交AC于点D。
连接BD,则BD将AC分为两部分,AD与DC之比即为黄金比例。
这种作图法不仅直观展示了黄金比例的存在,还体现了数学与几何美学的完美结合。
2. 代数计算法
对于需要更精确数值的情况,可以通过代数方式直接计算。已知黄金比例φ满足方程φ^2 - φ - 1 = 0,解此二次方程可得:
φ = (1 + √5) / 2 ≈ 1.61803...
及其互补比例1/φ = (√5 - 1) / 2 ≈ 0.61803...,二者均代表了黄金比例的不同表现形式。
三、黄金比例的应用领域
1. 自然界中的黄金比例
在自然界中,黄金比例无处不在,从植物叶片的排列、海螺壳的螺旋增长,到动物身体的比例设计,都能发现黄金比例的踪迹。这种自然选择下的美学优化,体现了宇宙间一种深层的和谐与秩序。
2. 建筑设计
在建筑领域,黄金比例被广泛应用于设计之中,从古希腊的帕特农神庙到现代的摩天大楼,设计师们利用黄金比例来创造视觉上的平衡与美感。例如,建筑物的长宽比、门窗与墙面的比例等,常采用黄金比例或其近似值进行设计,以达到最佳的视觉效果和空间感。
3. 艺术创作
在绘画、雕塑等艺术领域,艺术家们同样青睐黄金比例。达芬奇、米开朗基罗等大师的作品中,不难发现黄金比例的巧妙运用。它不仅帮助艺术家们构建出和谐、均衡的构图,还赋予了作品以永恒的美感和深刻的内涵。
4. 设计与视觉艺术
在现代设计与视觉艺术中,黄金比例更是不可或缺的设计原则之一。无论是平面设计中的排版布局、色彩搭配,还是网页设计中的界面设计、元素比例,都可以运用黄金比例来提升作品的吸引力和用户体验。
四、黄金比例背后的美学与数学原理
黄金比例之所以具有如此广泛的吸引力和影响力,与其背后深厚的美学与数学原理密不可分。从数学角度来看,黄金比例是斐波那契数列的极限比,这一数列在自然界和数学领域都有着广泛的应用和深远的意义。而从美学角度来看,黄金比例所体现的和谐与平衡之美,正是人类审美心理的自然反映和追求。
结语
综上所述,黄金比例作为一种独特的数学概念和美学标准,在自然界、建筑、艺术、设计等多个领域都发挥着重要的作用。通过几何作图或代数计算,我们可以轻松地得到黄金比例的数值,并在实际生活中灵活运用。更重要的是,理解黄金比例背后的美学与数学原理,有助于我们更好地欣赏和创造生活中的美。在这个充满变化与挑战的时代,让我们一同探索和应用黄金比例的智慧,为生活增添更多的和谐与美好。
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/07
-
02/07
-
02/07
-
02/07
-
02/07









