你知道吗？掌握这些导数公式，解题速度瞬间提升！必看的导数技巧汇总

在数学的浩瀚宇宙中，有一个既神奇又实用的工具，它像是一位引导我们探索函数变化奥秘的向导，那就是“导数公式”。想象一下，你手中拿着一张描述某物体速度随时间变化的图表，想要知道在某一刻这物体的加速度是多少，这时候，导数公式就像是你的超级放大镜，让你能精确捕捉到这一瞬间的动态变化。那么，接下来，我们就用轻松有趣的方式，一起揭开导数公式的神秘面纱。

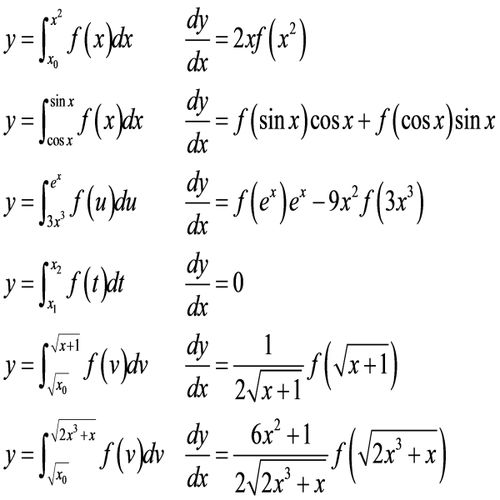
一、初识导数：速度与变化的秘密

首先，我们得从“为什么需要导数”说起。想象一下你正驾驶着一辆汽车，仪表盘上的速度计显示了你当前的速度，但如果你想知道加速或减速的快慢（即加速度），单凭速度计是不够的。这时候，我们就需要用到导数的概念。在数学上，导数描述了一个函数在某一点上的变化率，对于物理世界来说，它可以是速度的变化（加速度）、温度的变化率等等。

二、导数公式的诞生：从切线到极限

要理解导数公式，我们得从函数的图像说起。想象一下，你在一张纸上画了一个平滑的曲线，这条曲线代表了某个函数。现在，你选择一个点，想要知道这一点附近曲线是如何弯曲的，或者更具体地说，这一点的切线斜率是多少。切线斜率，在物理上可以理解为瞬间的速度或加速度，在数学上，则是该点处函数的变化率。

为了找到这个斜率，数学家们采用了“极限”的方法。简单来说，就是在该点附近取两个非常接近的点，计算这两点之间连线的斜率，然后让这两个点无限接近该点，最终得到的斜率就是该点处的导数。这个过程听起来复杂，但正是这一思想，孕育出了我们熟悉的导数公式。

三、基础导数公式：简单却强大

导数公式多种多样，但有几个基础公式是无论如何都绕不开的，它们就像是构建导数大厦的基石。

1. 常数函数的导数：如果你有一个常数函数f(x) = c（c是常数），那么它的导数f'(x) = 0。因为常数函数的图像是一条水平线，没有斜率变化。

2. 幂函数的导数：对于形如f(x) = x^n（n为实数）的函数，其导数为f'(x) = nx^(n-1)。这个公式告诉我们，幂函数的导数降低了原函数的幂次，并乘以幂次n。

3. 指数函数的导数：对于e^x（e是自然对数的底数，约等于2.718），其导数为(e^x)' = e^x。这意味着指数函数在其定义域内，无论x取何值，其导数都等于函数本身，这是一个非常特殊的性质。

4. 对数函数的导数：对于ln(x)（以e为底的对数），其导数为(ln(x))' = 1/x。这个公式告诉我们，对数函数在x=1附近变化最慢，而随着x的增大或减小，其变化率逐渐增大。

5. 三角函数的导数：正弦函数sin(x)的导数为cos(x)，余弦函数cos(x)的导数为-sin(x)。这些公式揭示了三角函数与其导数之间的紧密联系，也是三角学在微积分中广泛应用的基础。

四、导数公式的应用：从理论到实践

了解了这些基础导数公式后，你可能会好奇它们究竟有什么用。其实，导数公式的应用遍布各个领域，从物理学中的运动学问题，到经济学中的边际分析，再到工程学中的优化设计，无一不闪耀着导数公式的光芒。

物理学：通过导数公式，我们可以轻松求解物体的加速度、力的变化率等物理量，为力学、电磁学等领域的研究提供有力工具。

经济学：在经济学中，边际成本、边际收益等概念都与导数紧密相关。通过导数公式，企业可以精确计算每多生产一个单位产品所带来的成本或收益变化，从而做出更合理的决策。

工程学：在设计和优化过程中，工程师经常需要计算结构在不同载荷下的应力、变形等参数。这些参数的求解往往离不开导数公式的应用。

五、结语：探索不止，导数相伴

导数公式，这一看似简单的数学工具，实则蕴含着无限的力量和智慧。它不仅是连接微积分与实际应用的桥梁，更是我们探索自然界奥秘、解决现实问题的得力助手。在这个充满变化的世界里，让我们带着导数公式的钥匙，勇敢地开启每一扇探索之门，去发现更多未知的美好。

通过本文的介绍，希望你对导数公式有了更加直观和深入的理解。记住，数学之美在于其简洁与普适，而导数公式正是这一美学理念的完美体现。在未来的学习和生活中，不妨多多运用这些公式，去感受数学带来的乐趣和惊喜吧！