多边形内角和的快速计算方法

在探讨数学几何的广阔天地里，多边形内角和的求解是一个既基础又充满趣味性的课题。多边形，作为图形世界的重要成员，以其多变的边数和形态，展现了丰富的几何美感。那么，如何准确而高效地求出任意多边形的内角和呢？下面，我们将一步步揭开这个几何之谜。

多边形内角和初探

首先，我们需要明确“多边形”与“内角和”的基本概念。多边形是由三条或三条以上的线段（称为边）首尾顺次相连所组成的平面图形，这些线段相交形成的角即为多边形的内角。而多边形所有内角的度数之和，便是我们所说的多边形内角和。

从简单到复杂：从三角形开始

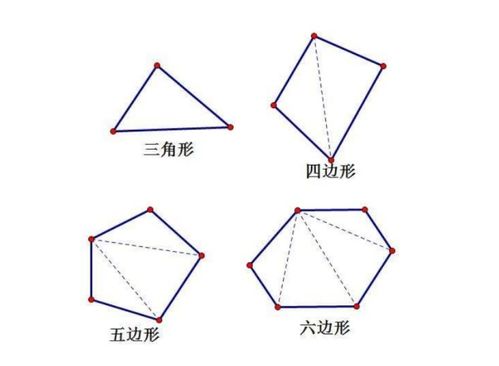
为了更好地理解多边形内角和的求解方法，我们可以从最简单的多边形——三角形入手。众所周知，三角形的内角和总是等于180°。这个结论可以通过多种方法证明，比如将三角形的一个角转化为平角（180°）的一部分，或者利用平行线的性质等。三角形作为多边形的基础，其内角和的固定性为我们后续的探索提供了坚实的基石。

推广到四边形

接下来，我们尝试将三角形的结论推广到四边形。四边形可以看作是由两个三角形组合而成（通过连接四边形的一条对角线）。由于每个三角形的内角和为180°，所以四边形的内角和就是两个三角形的内角和之和，即360°。这一发现启示我们：可以通过分割多边形为若干个三角形来求解其内角和。

多边形内角和的通用公式

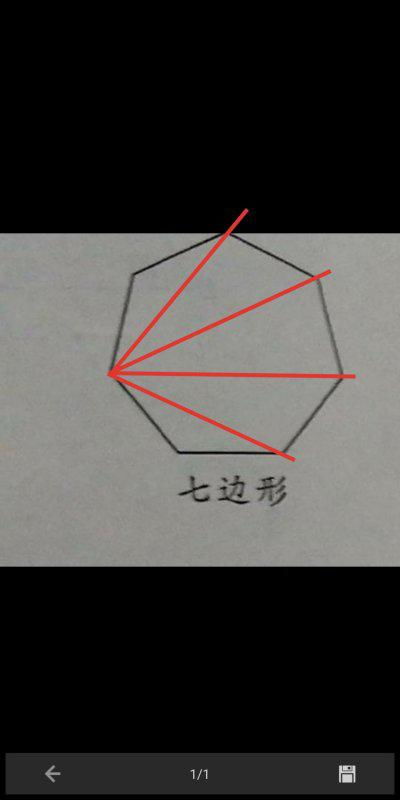
基于上述思路，我们可以进一步推导出多边形内角和的通用公式。对于一个n边形（n≥3），我们可以从任意一个顶点出发，画出(n-3)条对角线，将其划分为(n-2)个三角形。由于每个三角形的内角和为180°，所以n边形的内角和就是(n-2)个三角形的内角和之和，即：

\[ S = (n - 2) \times 180^\circ \]

这个公式简洁而有力，无论n取何值（n≥3），我们都能迅速计算出对应多边形的内角和。

实例演示

为了加深理解，我们不妨通过一个实例来演示公式的应用。假设有一个六边形，我们需要求出它的内角和。根据公式，将n=6代入得：

\[ S = (6 - 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ \]

所以，这个六边形的内角和为720°。

拓展思考

在掌握了多边形内角和的求解方法之后，我们还可以进一步思考：这个公式背后蕴含着怎样的几何规律？它是如何随着多边形边数的增加而发生变化的？此外，多边形的外角和也是一个有趣的课题，对于任意多边形而言，其外角和总是固定的，等于360°。这一性质与内角和的变化形成了鲜明对比，值得我们深入探究。

结语

通过以上的探讨，我们不仅学会了如何求解多边形的内角和，还领略了数学几何中的逻辑之美和推理之妙。多边形内角和的求解过程，不仅是对数学公式的简单应用，更是对数学思维能力和问题解决能力的锻炼。在未来的学习之路上，愿我们都能保持这份对未知的好奇与探索的热情，不断前行，在数学的海洋中遨游，发现更多的奥秘与美好。