ln公式具体是指什么?怎么理解和应用?
ln公式,即自然对数(Natural Logarithm)的表示方式,是数学中一个非常重要的概念,广泛应用于科学、工程、经济学等多个领域。简单来说,ln(x)表示以自然数e(约等于2.71828)为底的对数。下面,我们将深入探讨ln公式的定义、性质、应用以及一些基础的计算方法,旨在以直观易懂的方式,让读者对ln公式有一个全面的了解。
一、ln公式的定义
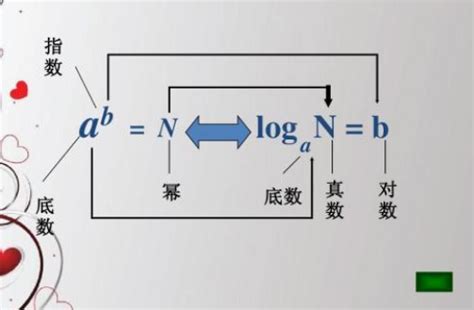
定义:ln(x)是自然对数函数,表示以自然常数e为底x的对数。换句话说,如果a^y = x(a>0且a≠1),那么y就是x以a为底的对数,记作y = log_a(x)。当a取值为e时,这个对数就被称为自然对数,记作y = ln(x)。
二、ln公式的性质
1. 定义域:ln(x)的定义域是(0, +∞),即x必须大于0。这是因为任何数的0次方都是1,而对数函数是指数函数的逆运算,所以不存在小于或等于0的自然对数。
2. 值域:ln(x)的值域是全体实数R。这意味着,无论x取何正值,ln(x)都能映射到实数轴上的某个点。
3. 单调性:ln(x)在其定义域内是单调递增的。即,如果x1 < x2,那么ln(x1) < ln(x2)。这一性质使得ln(x)在解决实际问题时非常有用,比如用于比较大小或进行排序。
4. 运算法则:
加法:ln(m*n) = ln(m) + ln(n)(m, n > 0)
减法:ln(m/n) = ln(m) - ln(n)(m > 0, n > 0)
幂运算:ln(m^n) = n*ln(m)(m > 0, n为实数)
换底公式:log_b(a) = ln(a) / ln(b)(a > 0, b > 0且b ≠ 1)
5. 导数:ln(x)的导数是1/x,这一性质在微积分学中非常重要,常用于求解与ln(x)相关的函数的导数。
三、ln公式的应用
1. 复利计算:在金融领域,ln(x)常用于计算复利。例如,如果你知道一笔投资在n年后的最终价值V,并且知道年利率r(以小数形式表示),那么你可以通过ln(V/P) = n*ln(1+r)来求解原始投资P,其中P是初始投资金额。
2. 半衰期计算:在化学和生物学中,ln(x)用于计算放射性物质的半衰期或生物体内药物浓度的下降速度。通过测量不同时间点的物质剩余量,可以利用ln(x)的性质来估算半衰期。
3. 经济学模型:在经济学中,ln(x)常用于构建模型以分析经济变量的增长或衰减趋势。例如,GDP增长率、失业率等数据的对数变换可以消除异方差性,使模型更加稳健。
4. 概率论与统计学:在概率论和统计学中,ln(x)经常出现在分布函数的表达式中,如正态分布、泊松分布等。此外,在最大似然估计等统计方法中,ln(x)也扮演着重要角色。
5. 生物学与生态学:在生态学和生物学研究中,ln(x)用于描述种群增长、生物量积累等过程。例如,Logistic增长模型中就使用了ln(x)来模拟种群数量随时间的变化。
四、ln公式的计算方法
1. 计算器或计算机程序:最直接的方法是使用计算器或计算机程序来计算ln(x)的值。大多数现代计算器和编程语言都内置了ln函数,只需输入x的值即可得到结果。
2. 泰勒级数展开:对于理论或编程爱好者来说,可以利用ln(x)的泰勒级数展开式来近似计算ln(x)的值。泰勒级数是一种将函数表示为无限项和的方法,对于ln(x)来说,其级数展开形式为ln(1+x) = x - x^2/2 + x^3/3 - ...(当|x| < 1时)。
3. 查表法:在过去,没有电子计算器的时代,人们会利用对数表来查找ln(x)的值。这种方法虽然效率较低,但在当时是一种重要的数学工具。
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/04
-
03/04
-
03/04
-
03/04
-
03/04












