根号2的计算结果及求解方法

当我们探索数学中的根号（也称为平方根）时，一个常见且基础的问题是：“根号2等于多少？怎么算？”这个问题看似简单，实则蕴含了数学的基本逻辑与无限不循环小数的奥秘。下面，我们将以直观且易于理解的方式，来解答这一疑问。

根号2的定义

首先，明确根号2（记作√2）的定义：它表示一个非负实数，这个实数的平方等于2。换句话说，我们需要找到一个数，这个数乘以自己（即平方）的结果为2。

初步估算

为了对√2有一个初步的认识，我们可以尝试通过估算来接近这个值。例如，我们知道1的平方是1，而2的平方是4，所以√2必然位于1和2之间。为了更精确地估算，我们可以考虑1和2之间的中点，即1.5，但1.5的平方是2.25，仍然大于2。于是我们继续寻找，可以发现1.4的平方是1.96，接近但小于2，而1.41的平方（约为1.9881）则更接近2。通过这种方法，我们可以逐步缩小范围，得到√2的一个近似值。

使用计算器

在日常生活和学习中，当我们需要快速且精确地知道√2的值时，最直接的方法就是使用计算器。无论是手机、电脑上的科学计算器，还是物理计算器，都能轻松给出√2的精确值，直到小数点后很多位。但这种方式虽然高效，却可能让我们错过探索根号背后数学原理的乐趣。

无限不循环小数

深入探索后，我们会发现√2其实是一个无限不循环小数，这意味着它的小数部分永远不会结束，也不会像1/3=0.333...那样有规律的重复。这一特性使得√2在数学中具有特殊地位，它不仅是无理数的代表之一，还与几何中的直角三角形、圆的性质等紧密相连。

几何直观

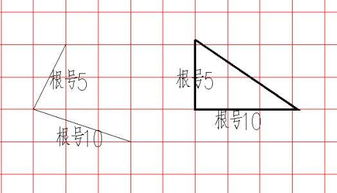
从几何角度来看，√2可以通过一个简单的构造来理解：想象一个边长为1的正方形，其对角线的长度就是√2。因为根据勾股定理（直角三角形中，直角边的平方和等于斜边的平方），这个正方形的对角线将正方形分为两个全等的等腰直角三角形，每个三角形的直角边长为1，斜边（即对角线）的长度则为√(1^2 + 1^2) = √2。

更高精度的计算方法

对于追求更高精度的数学家或科研工作者而言，他们可能会使用更复杂的数学方法来计算√2的近似值，比如牛顿迭代法（也称为牛顿-拉弗森方法）。这种方法通过不断迭代逼近真实值，可以得到任意精度的√2值。虽然其背后的数学原理较为深奥，但核心思想是利用函数的切线来逐步接近函数零点，从而求解方程的根。

结论

综上所述，根号2等于多少，不仅是一个数学问题，更是一个引领我们探索数学奥秘、理解无理数概念的入口。通过估算、计算器、几何直观以及更高级的数学方法，我们可以从不同角度接近这个神秘的数。记住，数学的魅力往往藏在这些看似简单却又深不可测的问题之中，等待着我们用好奇心和智慧去发掘。