揭秘！根号2背后的神秘数字，你真的了解它等于多少吗？

在数学的浩瀚宇宙中，隐藏着无数令人着迷的秘密与奇迹，其中，“根号2”这一简单而又深邃的概念，就像是夜空中最亮的星，引领着无数探索者步入智慧的殿堂。它不仅仅是一个数字，更是人类理性思维与自然界规律完美邂逅的见证。今天，就让我们一起揭开“根号2等于多少”这一问题的神秘面纱，走进一场跨越千年的数学之旅，感受那份纯粹而深邃的美。

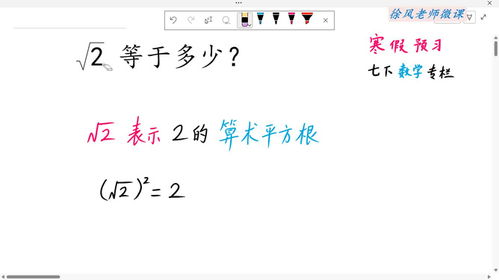
开篇：一场意外的发现

故事的起点，可以追溯到公元前5世纪的古希腊。在那个智慧绽放的时代，数学家们已经开始对数的性质进行深入的探讨。然而，直到毕达哥拉斯学派的兴起，一个看似简单的问题——“正方形的对角线与其一边的关系”，却意外地触动了数学世界的根基。

毕达哥拉斯学派深信“万物皆数”，即宇宙间的一切都可以归结为整数或整数之比（有理数）。然而，当他们尝试用这一理论去解释正方形的对角线长度时，却遭遇了前所未有的挑战。因为，他们发现，无论如何都无法将正方形的对角线长度表示为两个整数的比。这一发现，如同一颗石子投入平静的湖面，激起了层层涟漪，也标志着无理数概念的诞生。

探索：根号2的奥秘

那么，根号2究竟是多少呢？简单来说，根号2是一个数的平方根，这个数乘以自己等于2。在十进制下，根号2是一个无限不循环小数，大约等于1.4142135623730950...（这只是其小数点后的一部分）。这个特性让它成为了数学中第一个被明确识别的无理数，也因此成为了连接有理数世界与无理数世界的桥梁。

理性与直觉的碰撞

根号2的出现，不仅仅是数学上的一次突破，更是人类思维方式的一次革新。它挑战了当时人们的直觉——即所有事物的本质都可以用整数或整数之比来表达。这一挑战促使数学家们开始重新审视数学的基础，并逐渐发展出了更为宽泛和深邃的数学体系。

数学史上的里程碑

根号2的发现，在数学史上具有里程碑式的意义。它不仅推动了无理数理论的发展，还激发了数学家们对实数性质的进一步探索。欧几里得在《几何原本》中详细讨论了平方根的存在性和性质，为后来的数学研究奠定了坚实的基础。而到了19世纪，随着数学分析的发展，根号2的无理性得到了更加严格的证明，进一步巩固了其在数学体系中的地位。

现实生活中的应用

或许你会好奇，这样一个看似抽象的概念，在现实生活中有什么用处呢？实际上，根号2的应用无处不在。从建筑设计中的比例协调，到物理学中的振动分析；从经济学中的最优化问题，到计算机科学中的数据加密，根号2都以其独特的方式展现着它的价值。它就像是一位默默无闻的幕后英雄，默默地支撑着我们生活的每一个角落。

思维的启示

更重要的是，根号2的故事给予了我们深刻的思维启示。它告诉我们，在追求真理的道路上，永远不要拘泥于现有的框架和认知。正如毕达哥拉斯学派所经历的那样，当我们的直觉与事实发生冲突时，正是我们深化理解、拓展视野的绝佳时机。只有敢于挑战权威、勇于探索未知，我们才能不断推动人类文明的进步和发展。

结语：超越数字的意义

所以，当我们再次问起“根号2等于多少”时，或许我们应该更多地关注它背后的故事和意义。它不仅仅是一个数字那么简单，它是人类智慧与勇气的结晶；是理性与直觉碰撞产生的火花；是连接过去与未来的桥梁。在探索根号2的过程中，我们学会了质疑、学会了思考、学会了成长。而这，或许才是数学乃至整个科学探索的真正魅力所在。