怎样快速求出两个数的最小公倍数？

在这个充满数学奥秘的世界里，你是否曾为求解两个或多个数字之间的“桥梁”——最小公倍数（LCM，Least Common Multiple）而苦恼？或许，你正站在知识的十字路口，寻找那把开启数学新领域的钥匙。别担心，今天，我们就来一场别开生面的探索之旅，用轻松有趣的方式，揭开最小公倍数的神秘面纱，让你在享受学习的同时，也能轻松掌握这门技巧，成为朋友圈中的“数学小达人”！

一、初识最小公倍数：从“最小”到“公”的奇妙邂逅

想象一下，你有两块不同大小的拼图碎片，它们各自独立却又似乎能拼接成一幅更大的图画。这就像是两个数，它们各有特色，但当我们找到它们的“共同点”时，就能拼接出一个更加完整、包容的数字——这就是最小公倍数。

简单来说，最小公倍数就是两个或多个整数共有的倍数中最小的一个。它不仅仅是一个数字那么简单，更是数学中解决实际问题的一把利器。比如，当你需要同时购买某种商品的多个包装，而每种包装的数量又不同时，最小公倍数就能帮你计算出最少需要购买多少个，以确保每种包装都能被整除，避免浪费。

二、揭秘求最小公倍数的三大法宝

法宝一：列举法——直观易懂的入门级方法

这是最基础也是最直接的方法。只需将两个数（或多个数）的倍数一一列出，然后找到它们共同出现的第一个数，那就是最小公倍数。比如，求6和8的最小公倍数，你可以列出6的倍数：6、12、18、24...；再列出8的倍数：8、16、24...。很明显，它们第一个共同的倍数是24，所以6和8的最小公倍数是24。

法宝二：分解质因数法——深入骨髓的理解

这个方法虽然稍显复杂，但一旦掌握，便能让你对最小公倍数有更深刻的理解。首先，将每个数分解成质因数的乘积。然后，取各质因数的最高次幂相乘，所得的结果即为最小公倍数。例如，求12和18的最小公倍数。12=2^2×3，18=2×3^2，取最高次幂相乘得2^2×3^2=36。

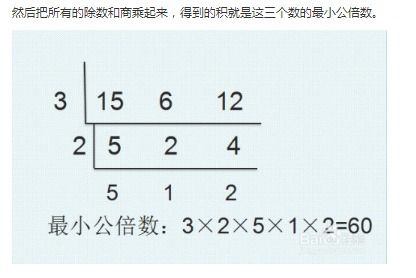
法宝三：短除法——高效快捷的秘籍

对于较大的数或者需要快速求解的情况，短除法无疑是最好的选择。将需要求最小公倍数的数列出来，用它们的公有质因数去除，直到商互质为止。然后，将所有除数和最后的商相乘，结果即为所求的最小公倍数。这种方法在解决复杂问题时尤其高效。

三、实战演练：让理论飞翔在解题的天空

理论知识学得再好，不实践也是枉然。现在，就让我们通过几道例题，将所学知识付诸实践吧！

例1： 求24和36的最小公倍数。

解析： 使用分解质因数法，24=2^3×3，36=2^2×3^2。取各质因数的最高次幂相乘得2^3×3^2=72。

例2： 有一间教室，每行可以坐8个学生，每列可以坐9个学生。请问，如果要让每个学生都有座位，这间教室至少需要多少个座位？

解析： 这个问题其实就是在求8和9的最小公倍数。使用短除法，8和9互质，直接相乘得72。所以，教室至少需要72个座位。

四、趣味拓展：最小公倍数在生活中的应用

你以为最小公倍数只是书本上的枯燥知识吗？错了！它其实无处不在，与我们的生活息息相关。比如，在音乐中，音符的时值关系就涉及到最小公倍数。当两种不同节奏的音符组合在一起时，为了保持音乐的和谐流畅，往往需要找到它们时值的最小公倍数，以确保每个音符都能“完美融合”。

再比如，在编程中，循环和数组的操作也常常会用到最小公倍数来优化算法，提高程序效率。可以说，最小公倍数是连接数学与现实世界的桥梁，让我们的生活更加便捷、高效。

结语：掌握最小公倍数，开启数学新世界的大门

通过今天的探索之旅，相信你已经对最小公倍数有了更加全面而深刻的认识。无论是基础的列举法、深入骨髓的分解质因数法，还是高效快捷的短除法，都是你手中的宝贵工具。在未来的学习和生活中，当你再次遇到与最小公倍数相关的问题时，希望你能够游刃有余地解决它们，甚至还能举一反三，发现更多数学的乐趣和奥秘。

记住，数学不仅仅是一门学科，更是一种思维方式，一种探索世界的工具。掌握了数学，你就拥有了一把打开新世界大门的