探索数学基础：你真正了解角的概念吗？

在探索数学的广袤领域中，"角"这一概念如同基石一般，稳固而基础，它不仅是几何学的重要组成部分，也是日常生活中无处不在的几何元素。当我们提及“角的概念”，实际上是在揭开一个既简单又深奥的数学之谜，这个谜面广泛影响着我们对形状、方向以及空间关系的理解。

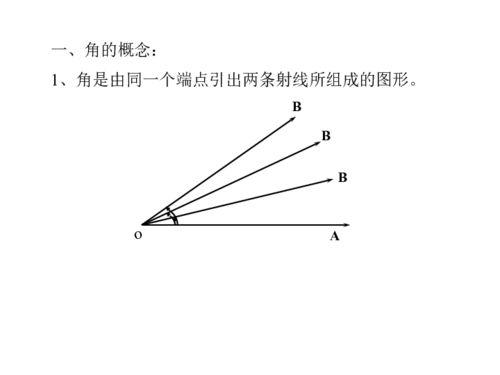
角：定义与直观感受

首先，让我们从直观感受出发，想象一下一个最常见的场景：当你站在一个十字路口，面前有两条相交的道路，它们之间就形成了一个“角”。在几何学中，角被正式定义为“由两条具有公共端点的射线所夹的平面部分”。这里，“射线”指的是从一点出发并沿某一方向无限延伸的线段，而“公共端点”则是这两条射线相交的那一点，我们称之为角的“顶点”。

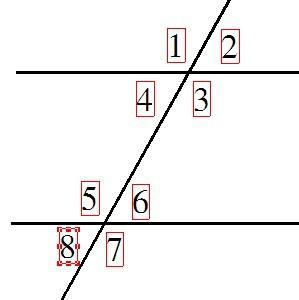
角的度量与分类

为了更精确地描述角，我们需要引入度量的概念。最常见的角的度量单位是“度”（°），此外还有“弧度”等其他度量方式，但在日常学习和生活中，“度”的应用最为广泛。根据度数的大小，角可以分为以下几类：

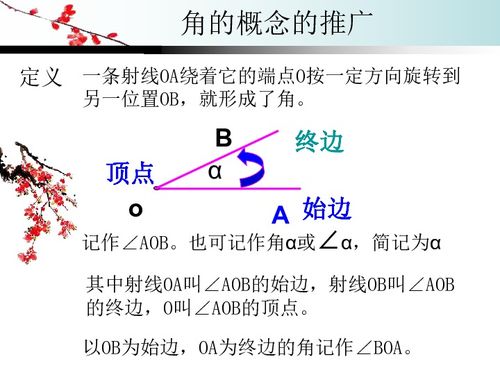
1. 锐角：度数小于90°的角。它们给人以尖锐、紧凑的视觉感受，如三角形中最小的那个内角。

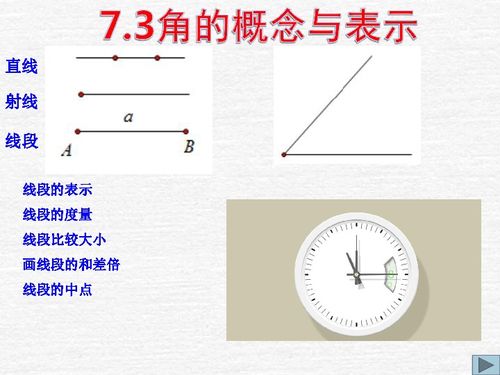
2. 直角：度数恰好为90°的角。它代表了垂直关系，是许多图形和建筑设计中不可或缺的元素，如房间的墙角、书本的直角边等。

3. 钝角：度数大于90°但小于180°的角。钝角给人以宽阔、舒缓的感觉，常见于某些特殊形状和设计中。

4. 平角：度数为180°的角。在视觉上，它看似是一条直线，但实际上由同一条射线绕其端点旋转180°形成，仍属于角的范畴。

5. 周角：度数为360°的角。它表示射线绕其端点旋转一整圈，虽然在日常讨论中较少直接提及周角作为角的一种，但它在数学和物理领域有着重要应用。

角的性质与应用

角不仅有着明确的定义和分类，还具备一系列重要的性质，这些性质在解决实际问题时发挥着关键作用。例如：

角的和与差：在几何图形中，多个角之间的关系可以通过加法或减法来表示，这有助于我们计算复杂图形的内角和或外角和。

角的平分线：从一个角的顶点出发，将该角分为两个相等的小角的射线称为角的平分线。它在构造对称图形、证明几何定理时极为有用。

角的互补与互余：如果两个角的度数之和为90°，则它们互为余角；若和为180°，则互为补角。这些关系在解决直角三角形和其他特殊角度问题时非常关键。

此外，角的概念还广泛应用于工程、建筑、设计等多个领域。在建筑设计中，合理利用角度可以创造出既美观又实用的空间布局；在机械设计中，角度的精确控制是实现机器正常运转的关键；在艺术创作中，角度的变化能够赋予作品独特的视觉效果和情感表达。

角的探索与发现

随着数学学习的深入，我们还会遇到更多关于角的复杂问题和高级概念，如角的三角函数、多边形的内外角和定理、圆的扇形与圆心角等。这些概念的引入，不仅丰富了我们对角的认识，也为我们打开了一扇通往更高层次数学世界的大门。

在探索角的过程中，我们不难发现，角虽然是几何学中的一个基本概念，但它却蕴含着无限的奥秘和可能。每一次对角的深入理解，都是对自然界和人类智慧的一次致敬。因此，无论你是数学爱好者还是初学者，都请保持对角的好奇和热情，因为在这个看似简单的几何元素中，隐藏着通往广阔知识海洋的秘密通道。

综上所述，“角的概念”不仅是几何学的基础，更是连接数学与现实世界的桥梁。通过理解角、探索角、应用角，我们能够更加深入地认识这个世界的形状、结构和规律。